Методы оценки погрешности измерения координат в комплексированных системах…
17
4. Сгенерировать
v
N
наборов параметров калибровки системы
v
,
соответствующих нормальному распределению
(
)
,
.
v
v Σ
N
5. Используя полученную в п. 4 выборку, вычислить
1
= [
]
v
E
−
b
v v
и
1
= [
].
v
−
Σ Σ v v
6. Определить матрицу ковариации
x
Σ
аналитическим методом,
используя выражения (5) и (8).
7. Аналогично определить аналитическим методом вектор смеще-
ния
1
x
b
и матрицу ковариации
1
x
Σ
для данной выборки, используя
выражения (4), (5) и (7), (8), где вместо
p
Σ
и
v
Σ
следует подставить
1
p
Σ
и
1
v
Σ
соответственно. Вектор смещения
1
1
1
ˆ
ˆ
=
.
x
p
v
∂
∂+
∂
∂
x
x
b
b
b
p
v
8. Найти
x
N
оценок трехмерных координат точки ˆ ,
x
используя
алгоритм триангуляции вида (2), вектора
p
и
v
комбинируются в
соответствии с определенным правилом.
9. Используя полученную в п. 8 выборку, вычислить
2
ˆ = [
]
x
E
−
b
x x
и матрицу ковариации
2
ˆ = [
].
x
−
Σ Σ x x
Поскольку для получения надежных результатов необходимо
большое число точек
,
x
N
такой анализ нецелесообразно проводить
для всех рассматриваемых точек рабочего объема. Учитывая предпо-
лагаемый характер распределения погрешности, выбрано несколько
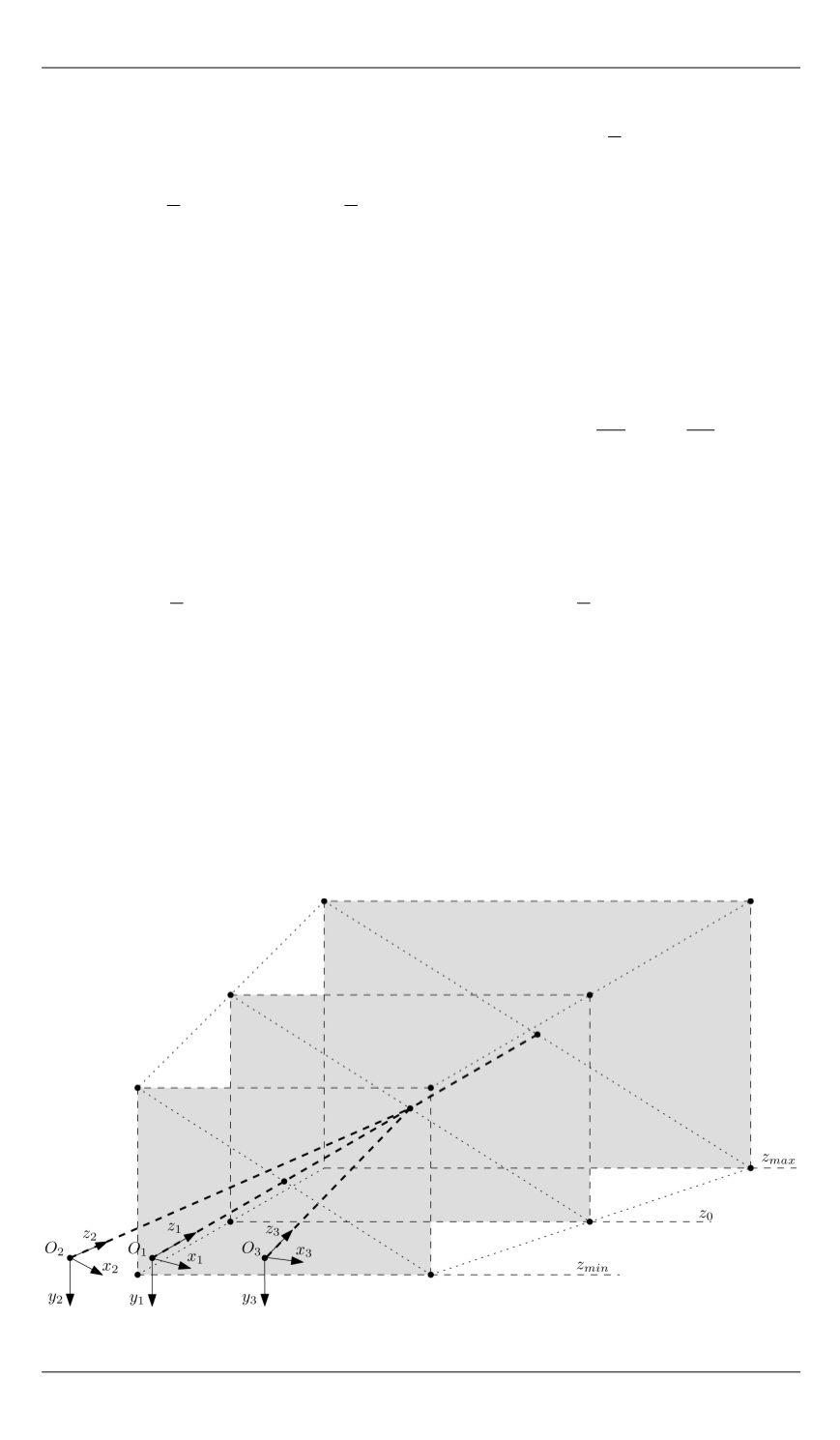
сечений рабочего объема и проведен анализ для отдельных точек
этих сечений (рис. 4). Выбор достаточного числа расчетных точек
для проверочного расчета определялся требуемой точностью пред-
ставления и характером распределения погрешности в пределах ра-
бочего объема.
Рис. 4.
Выбор точек рабочего объема для анализа


