
Исследование оптимального трехимпульсного перехода на высокую орбиту…
Инженерный журнал: наука и инновации
# 9·2017 3
определяются в два этапа. При этом
x
1
соответствует
i
= 1 –
x
1
= γ
(или α), а
x
2
— i
= 2 –
x
2
= γ’ (или α’).
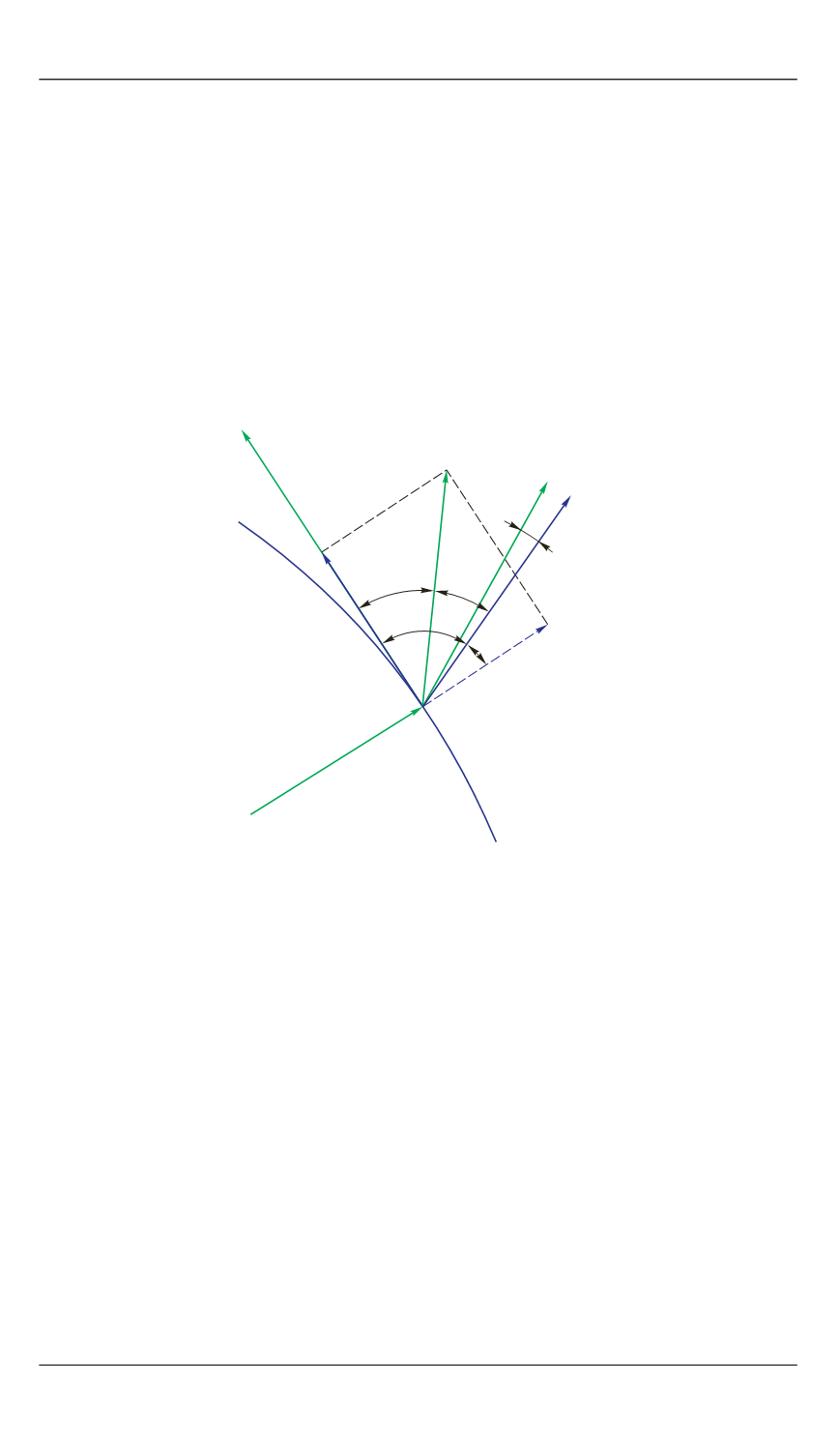
Ориентация вектора тяги задается в оскулирующей плоскости
(
rn
) углами тангажа γ или атаки α и в направлении, ортогональном
плоскости (
rn
), — углом рыскания ψ (рис. 1). Здесь (
rn
) — плоскость,
образованная ортами
r
° и
n
°, получаемыми при переходе от текущего
вектора состояния в эпоху J2000.0 к вектору в орбитальной системе
координат
rnb
.
Угол тангажа γ отсчитывается в положительном
направлении от радиуса-вектора
r
до вектора тяги
P
и определяется
как γ =
/2 –
– α, где
— угол наклона вектора скорости к трансвер-
сали
n
°, γ — угол наклона вектора тяги к трансверсали
n
°.
Рис. 1.
Схема определения углов ориента-
ции тяги (стрелки показывают положитель-
ные направления углов)
Оптимальные значения двух параметров в рамках законов управ-
ления (1), координат двухмерного вектора
x
(
x
1
,
x
2
), определяются
в два этапа: сначала используется метод «градиентного спуска», за-
тем значения параметров, полученные после его применения, уточ-
няются методом Давидсона — Флетчера — Пауэлла [4, 5]. В настоя-
щей работе применен вариант Пауэлла; далее по тексту такую
разновидность метода будем называть методом Пауэлла (квазинью-
тоновским методом или квазиньютоновским методом Пауэлла). Па-
раметр
x
1
соответствует индексу
i
= 1, тогда
x
1
=
(или
), а
x
2
— ин-
дексу
i
= 2, т. е.
x
2
=
(или
).
Сначала, в методе «градиентного спуска», минимизируется функ-
ционал
F
(например, длительность работы двигателя на активном
участке
t
f
):
V
t
V
r
P
r
n
O
V
P
















