
Е.С. Гордиенко
10
Инженерный журнал: наука и инновации
# 9·2017
=
0
m
i
+
,
m
f
i
затем алгоритм оптимизации повторяется. Так происхо-
дит до тех пор, пока не выполнится условие:
m
f
i
<
ઽ
i
. Задача сходит-
ся за пять-шесть глобальных итераций.
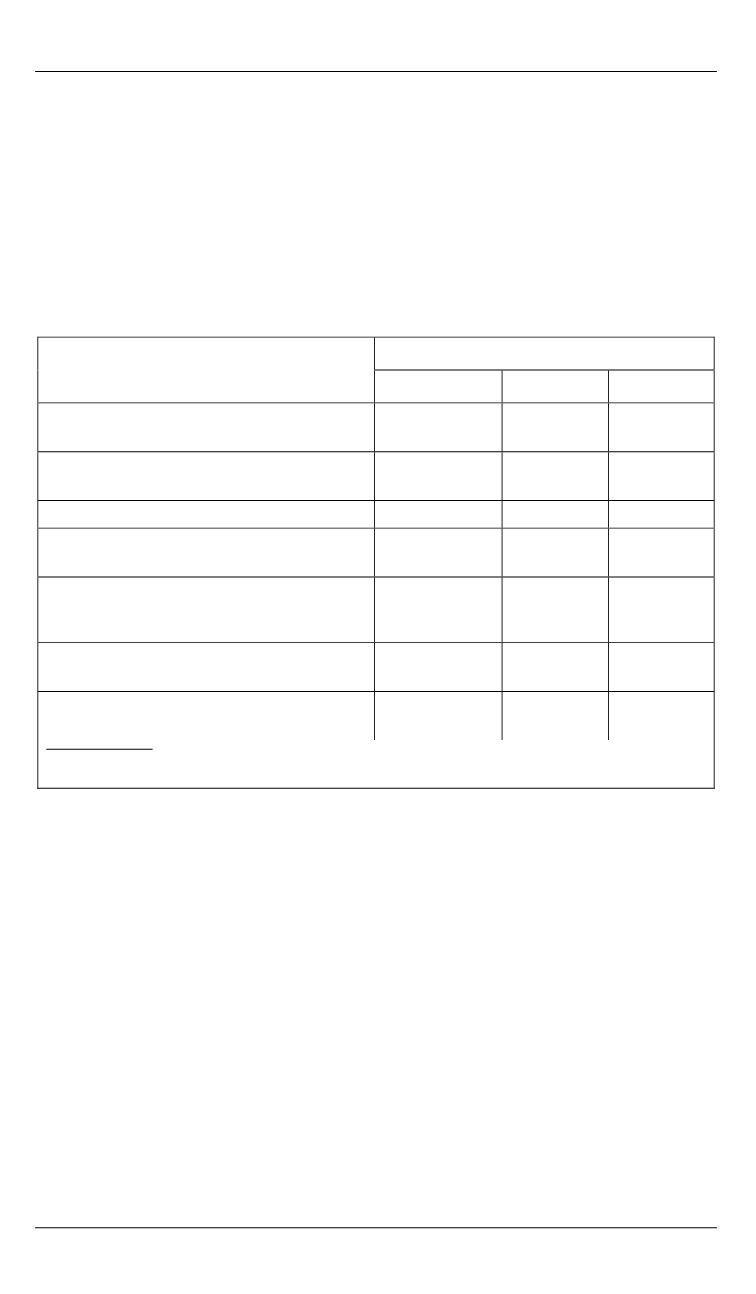
Основные результаты оптимизации трехимпульсного перехода на
орбиту ИСЛ приведены в табл. 1.
Таблица 1
Результаты оптимизации трехимпульсного перехода на орбиту ИСЛ
квазиньютоновским методом Пауэлла при управлении по углу γ
Параметр
Импульс
первый
второй
третий
Момент приложения импульса
T
имп
(UTC)
29.09.2016
3:32:32
01.10.2016
9:06:15
03.10.2016
4:48:15
Время до пролета апсидальных точек*
t
0
T
, с
–6,208
29216,805
–0,168
Конечная масса КА
m
f
, кг
1912,9069
1867,2673 1690,6738
Импульс скорости Δ
V
х
, м/с
i
5
= 52,984256
188,0468
70,7356
291,0173
Угол тангажа в момент сообщения
импульса γ, град
∆
i
f
5
= 0,0009838°
270,1368
91,0197
270,0017
Угол атаки в момент сообщения
импульса α
,
град
180,13553
19,52027
180,00906
Расстояние до центра Луны
r
f
, км
i
5
= 52,9852398°
1838,572
44121,591
6000,001
* Для импульсов:
первого
—
1,
второго
—
1,
третьего
—
2.
Из табл. 1 видно, что оптимальные моменты приложения импуль-
сов смещаются из апсидальных точек орбит. Для
первого
и
третьего
импульсов сдвиг по времени относительно перицентров мал по срав-
нению с периодом орбиты, для
второго
он составил ~8 ч. При этом
точки приложения
первого
и
третьего
импульсов смещаются
в область до пролета периселения, а
третьего
— в область после
пролета апоселения. В данном случае при движении КА по траекто-
рии трехимпульсного перехода селенографическое наклонение под
действием возмущений (см. формулу (8)) растет. Поэтому смещение
точки приложения
второго
импульса
P
2
по орбите
Т
1
в область после
пролета апоселения ведет к увеличению наклонения
i
3
и уменьшению
подлетного
i
0
на ~2,4°. Углы тангажа γ и атаки
после приложения
первого
и
третьего
импульсов составили γ
270° и
180°, а по-
сле приложения
второго
— γ
91° и
19,8°.
















