
Моделирование взаимодействия мобильного робота и опорного основания…
Инженерный журнал: наука и инновации
# 12·2016 5
Алгоритм EPA (Expanding Polytope Algorithm).
Суть EPA со-
стоит в получении фигуры, состоящей только из внешних вершин
CSO и содержащей начало координат (ABCDE на рис. 3). Предлага-
ется [4] использовать в качестве начальной фигуры симплекс, полу-
ченный по итогам работы GJK. Затем необходимо попытаться уда-
лить ближайшую к началу координат сторону (ABD) и добавить к
фигуре с помощью
вспомогательной функции
новую, как можно бо-
лее дальнюю вершину
E
. Операцию повторяют, пока не будет полу-
чена вершина, уже имеющаяся в фигуре EPA. Расстояние от бли-
жайшей стороны фигуры (ABC на рис. 3) до начала координат (по
нормали) называют вектором проникновения многогранников
pnt
r
.
Определение контактных точек.
Зная направление взаимного
проникновения многогранников, можно найти точки их контакта.
Обычно для этого применяют алгоритм обрезки (Clipping Algorithm
[7]). Реализация алгоритма для модели, рассматриваемой в данной
статье, была выполнена в ниже следующей последовательности.
1. Нахождение крайних в направлении контакта точек много-
гранников.
2. Поиск на обоих многогранниках треугольников, содержащих
крайние точки и имеющих нормали, самые близкие к направлению
контакта
pnt
r
. Плоскость «наиболее перпендикулярного» треугольни-
ка называется набегающей (incident plane [7],
1
на рис. 4), плоскость
другого многогранника — опорной (reference plane [7],
2
на рис. 4).
Считается, что точки контакта находятся на опорной плоскости.
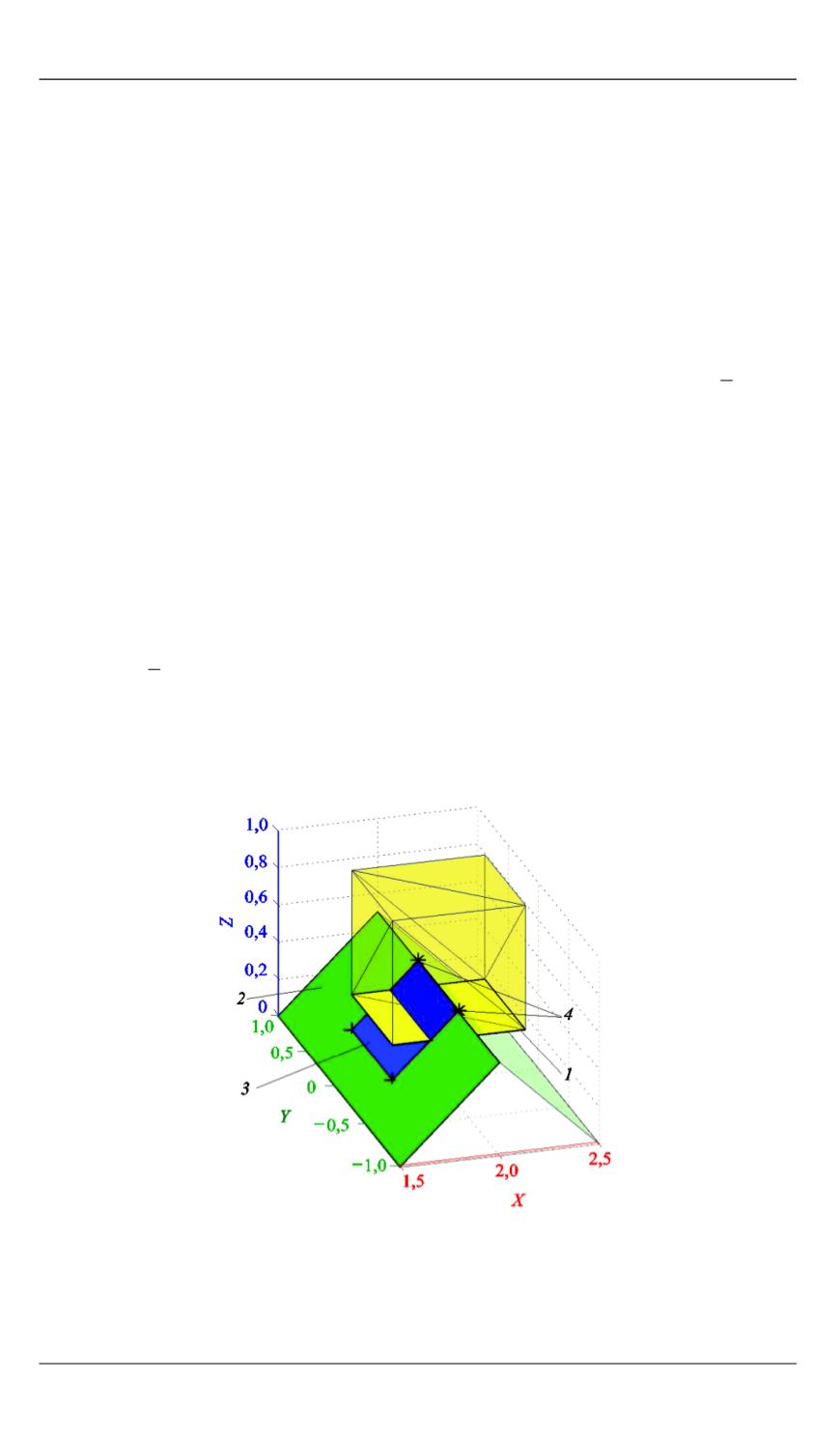
Рис. 4.
Поиск точек контакта:
1
— набегающая плоскость;
2
— опорная плос-
кость;
3
— пересечение проекций многоугольни-
ков;
4
— контактные точки
















