
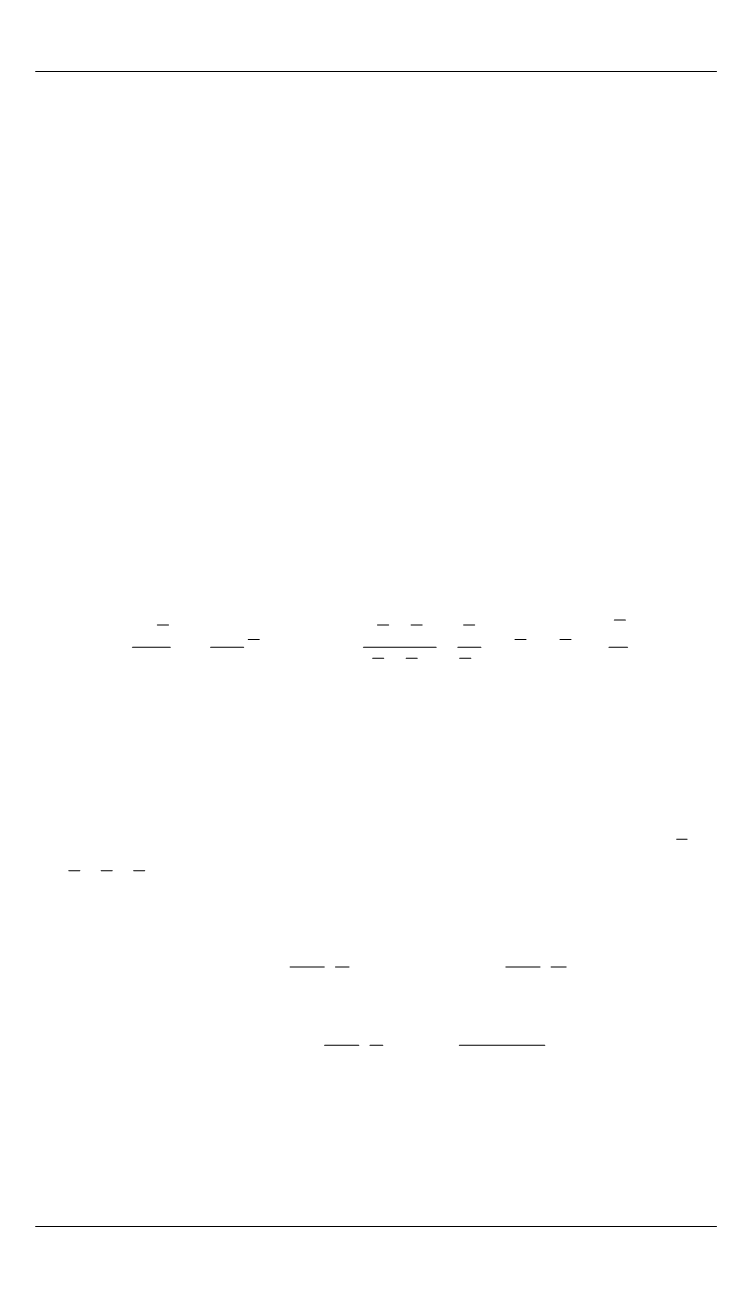
Е.С. Гордиенко, В.В. Ивашкин
8
Инженерный журнал: наука и инновации
# 3
⋅
2016
Энергетически такой переход лучше, чем одноимпульсный.
Выигрыш в характеристической скорости и конечной массе КА для
трехимпульсного перехода по сравнению с одноимпульсным в
центральном поле Луны при величине
r
2
= 50 000 км составит:
δ
V
= 67,008 м/с и δ
m
= 38,251 кг; а при
r
2
= 60 000 км: ∆
V
f
= 543,459 м/с,
δ
V
= 72,238 м/с, δ
m
= 41,273 кг.
Отметим, что
далее будут необходимы характеристики перехода
при
r
2
= 45 000 км. Приведем их: ∆
V
f
= 551,632 м/с, ∆
V
1
= 187,128 м/с,
∆
V
2
= 67,626 м/с, ∆
V
3
= 296,878 м/с, δ
V
= 64,035 м/с, δ
m
= 36,552 кг.
Модель поля и уравнения движения КА при учете возмуще-
ний.
Расчет траектории перелета к Луне при учете возмущений
осуществляют в рамках задачи четырех тел (КА, Земля с учетом ее
сжатия (т. е. 2-й зональной гармоники
J
2
), Луна с учетом ее
нецентральности в разложении в ряд 8×8 и Солнце) и определяют
численным интегрированием системы дифференциальных уравнений
движения точки в невращающейся геоцентрической геоэквато-
риальной системе прямоугольных координат
OXYZ.
При этом
используют среднее равноденствие и средний геоэкватор стандартной
эпохи
J
2000.0. Дифференциальные уравнения, описывающие движение
КА, имеют вид:
2
2
2
3
3 3
1
μ
μ
,
|
|
=
−
= − +
− + + +
−
∑
M
i
i
i
E M
i
i
i
d r
r r r
P
r
a a
m
dt
r
r r
r
(7)
где
r
— селеноцентрический радиус-вектор КА; μ
м
— гравитационный
параметр Луны; μ
i
и
r
i
— гравитационные параметры и радиус-векторы
возмущающих небесных тел (Земля, Солнце), где
i
= 1 соответствует
возмущениям от притяжения Земли, а
i
= 2 — притяжению Солнца;
{ ,
,
}
M
Mx
My
Mz
a a a a
=
— возмущающее ускорение, вызванное нецентраль-
ностью поля тяготения Луны в разложении в ряд 8×8;
E
a
=
{ , , }
Ex
Ey
Ez
a a a
=
— возмущающее ускорение, вызванное нецентраль-
ностью поля тяготения Земли,
2
2
0
0
2
2
2
2
2
0
0
2
4
5
5
[ 1 ] ,
[ 1 ] ,
5
3
[ 3 ] ,
,
2
Ex
E
Ey
E
E e
Ez
E
E
z x
z y
a a
a a
r
r
r
r
z z
J R
a a
a
r r
r
= − +
= − +
µ
= − +
=
(8)
где
R
e
,
J
2
— экваториальный радиус и коэффициент 2-й зональной
гармоники геопотенциала Земли.
Векторы состояния Луны и Солнца определяем из табличных
эфемерид DE-405 [4]. В исследовании использованы следующие
константы: μ
E
= 398600,4481 км
3
/с
2
; μ
M
= 4902,79914 км
3
/с
2
; μ
s
=
















