
Анализ оптимального трехимпульсного перехода на орбиту искусственного спутника Луны
Инженерный журнал: наука и инновации
# 3
⋅
2016 3
где
V
1
— величина вектора скорости в периселении подлетной
гиперболической орбиты.
Время перелета с орбиты ИСЗ на орбиту ИСЛ составляет
примерно 4,6 суток, скорость на бесконечности при подлете к Луне
821 627
∞
= ,
V
м/с,
1
1519 651
= ,
V
м/с. В нашем случае
r
f
=
a
f
= 6000 км,
V
f
= 903,954 м/с. Тогда
1
= 615 697
∆
,
imp
V
м/с.
Конечную массу после торможения вычисляем по формуле
Циолковского:
m
f
= 1653,064 кг. (Здесь и далее в расчетах
использованы следующие параметры ДУ:
P
= 420 кГс,
P
уд
= 298,7 с,
W
e
=
P
уд
g
0
, где
g
0
= 9,80665 м/с
2
— ускорение свободного падения.)
Трехимпульсный вариант торможения.
Известно, что в случае
кеплеровского поля Луны при достаточно большом радиусе орбиты
ИСЛ энергетически оптимальным будет трехимпульсный перелет с
начальной селеноцентрической орбиты подлета к Луне на конечную
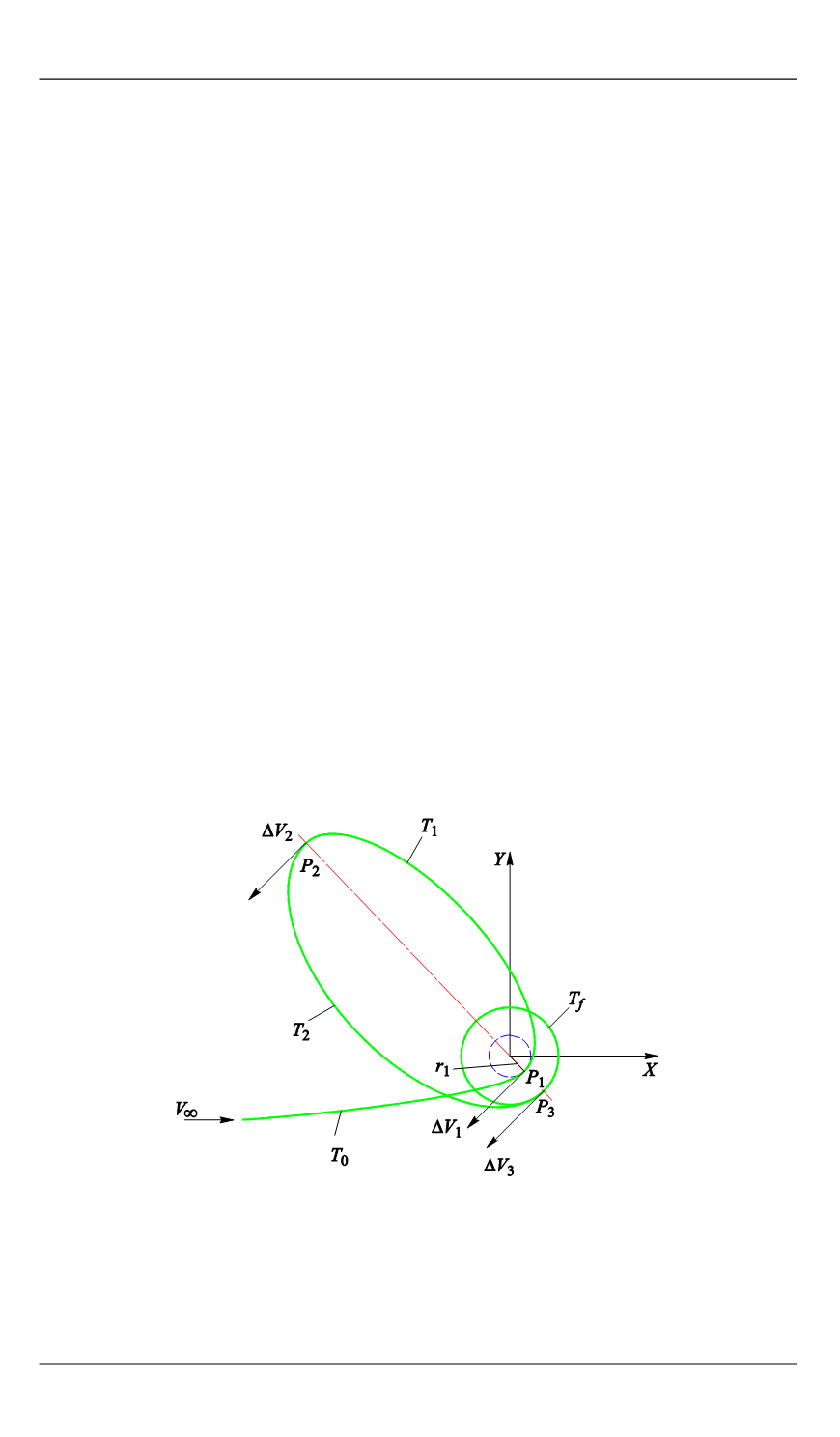
орбиту ИСЛ [1–3]. Рассмотрим схему трехимпульсного маневра у
Луны (рис. 1).
Первый, тормозной импульс
∆
V
1
сообщается в периселении
Р
1
начальной гиперболической орбиты
Т
0
. После этого КА летит от
Луны к точке
Р
2
приложения второго импульса
∆
V
2
на эллиптической
орбите
Т
1
далеко от Луны. Второй импульс — ускоряющий —
увеличивает расстояние в периселении
Р
3
эллиптической орбиты
Т
2
до радиуса
r
f
конечной орбиты ИСЛ
Т
f
. Третий, тормозной импульс
∆
V
3
переводит КА на конечную орбиту ИСЛ
Т
f
. Все импульсы —
апсидальные.
Рис. 1.
Трехимпульсный маневр торможения КА у Луны
Анализ задачи трехимпульсного перехода.
Анализ проведен в три
этапа. На первом рассмотрено движение КА в центральном ньюто-
новском гравитационном поле притяжения Луны (кеплеровский
случай), в импульсном приближении.
















