
Анализ оптимального трехимпульсного перехода на орбиту искусственного спутника Луны
Инженерный журнал: наука и инновации
# 3
⋅
2016 7
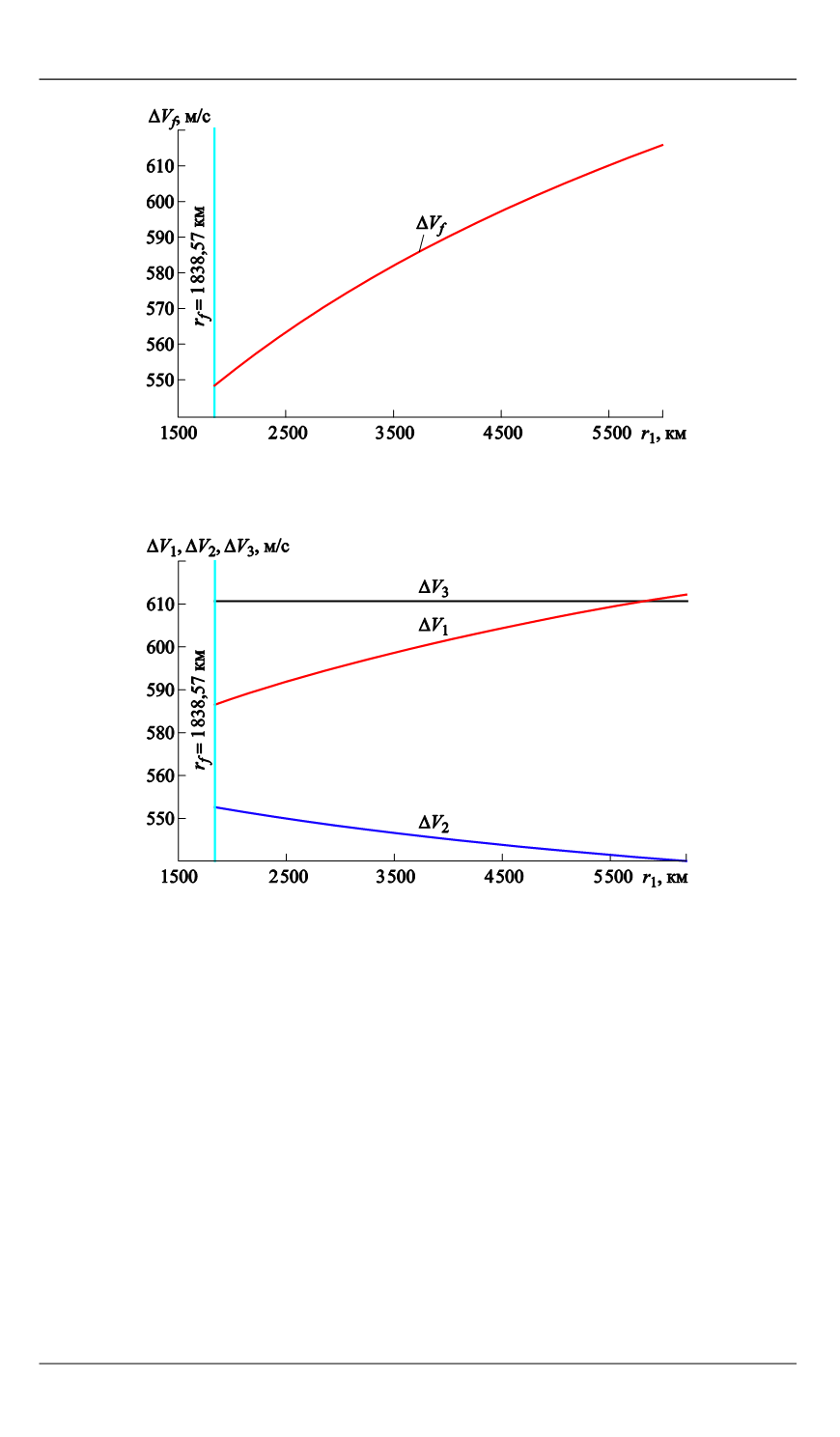
Рис. 4.
Зависимость суммарной величины трехимпульсного
перехода от величины
r
1
Рис. 5.
Зависимости величин первого (
красная кривая
),
второго (
синяя кривая
) и третьего (
черная кривая
) импульсов
перехода от величины
r
1
Из анализа рис. 4 и 5, а также формул ∆
V
1
=
f
(
r
1
,
r
2
), ∆
V
2
= f
(
r
1
,
r
2
,
r
3
),
∆
V
3
= f
(
r
2
,
r
3
) следует, что с увеличением радиуса
r
1
величина
суммарного импульса скорости монотонно возрастает. Таким образом,
критерию минимизации характеристических затрат соответствует
условие максимально близкого пролета КА от центра Луны в точке
Р
1
.
Поэтому для радиуса пролетной орбиты выбираем величину
r
1
=
= 1838,57 км.
Итак, оптимальным считаем вариант трехимпульсного перехода в
центральном поле Луны при следующих значениях параметров,
характеризующих траекторию перелета КА на орбиту ИСЛ:
r
1
=
=1838,57 км,
r
2
= 50 000 км,
r
3
= 6000 км, ∆
V
f
= 548,689 м/с, масса КА
m
f
= 1691,315 кг.
















