Ю.П. Корнюшин, Н.Д. Егупов, П.Ю. Корнюшин
10
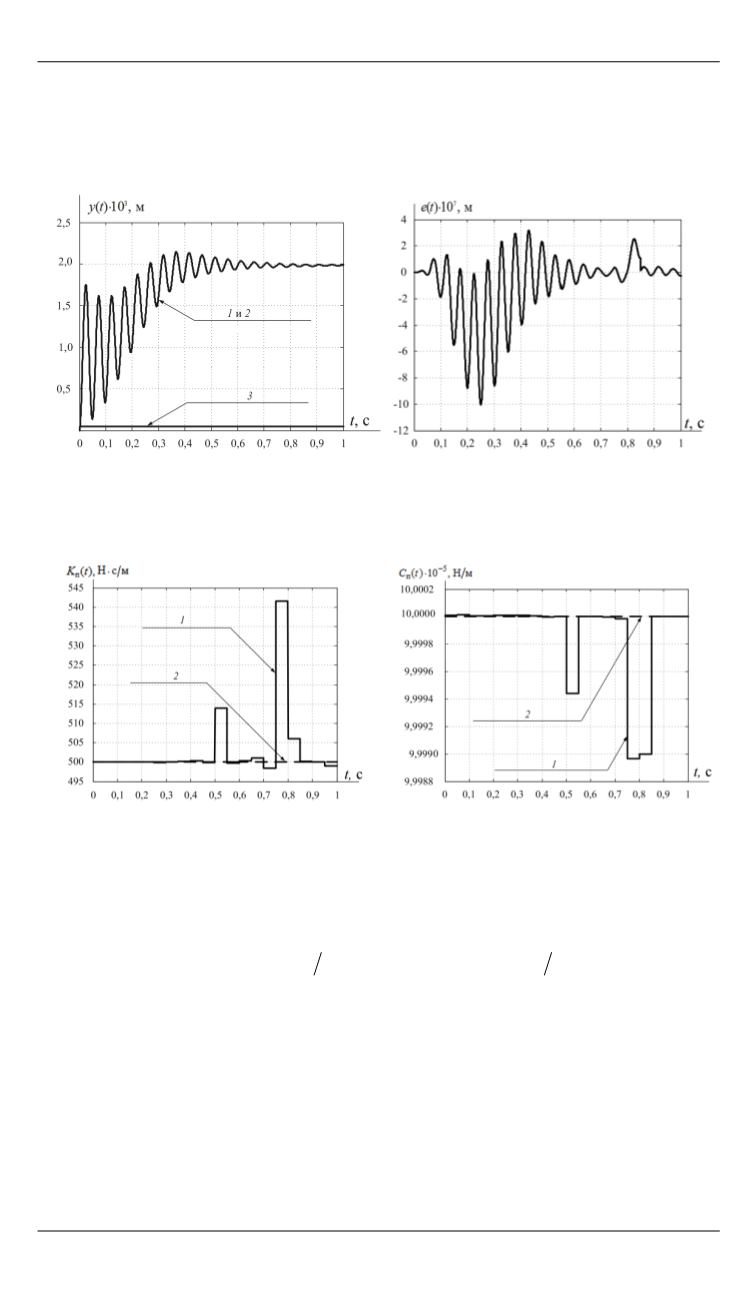
лученной расчетным путем. На рис. 3 и 4 приведены графики изме-
нения идентифицируемых параметров
п
K
и
п
C
на 10-й итерации и
их точные значения.
Рис. 1.
Выходной сигнал
( ) :
y t
1
– измеренное значение;
2
– вычислен-
ное значение для 10-й итерации; 3 –
начальное приближение
Рис. 2.
Разность ( )
e t
между точным
значением выходного сигнала и
его оценкой
Рис. 3.
Изменение параметра
п
K
:
1
– расчетное значение;
2
– точное зна-
чение
Рис. 4.
Изменение параметра
п
C
:
1
– расчетное значение;
2
– точное
значение
На 10-й итерации получены следующие усредненные значения
п
K
и
п
C
:
п.ср
503, 04 Н с м ,
K
5
п.ср
9,9999 10 Н м
C
.
Выводы.
1. Моделирование на других примерах показало эффек-
тивность предлагаемого алгоритма идентификации. Полученные ре-
зультаты с высокой точностью совпали с результатами натурных,
физических экспериментов.
2. Поскольку процесс идентификации, определенный схемой ли-
неаризации Ньютона — Канторовича, является итерационным, то для
получения результатов с высокой точностью (верность данных) часто
требуется достаточно большое количество итераций. Критерием


