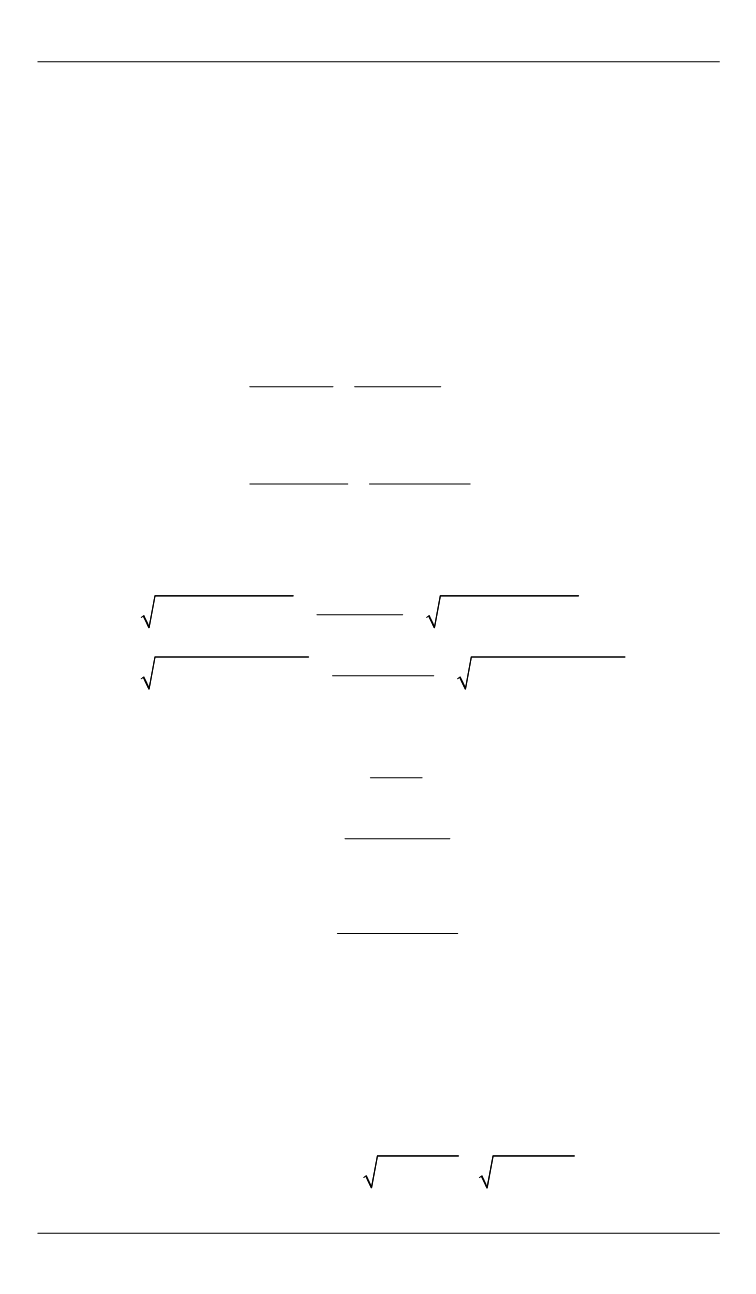
П.В. Храпов
14
1
2
1
1
0
;
2
2 ;
.........................
2
2 ;
0
.
n
n
n
y b
b y y b
b y y
b
h y b
(19)
При фиксированных переменных
1
, ...,
n
y y
переменные
1
, ...,
n
x x
могут принимать следующие значения:
1
2
2
2 1
2
1
2
2
2
2
1
1
2
2
0
;
(
) (
) 1;
4
4
.........................
(
) (
) 1.
4
4
n
n
n
n
x L
x x
y y
a
b
x x
y y
a
b
Перепишем (19) в виде
1
2
2
2
2
2 1
2
1
2
1
2
2
2
2
1
1
1
0
;
(
)
4 (
)
4 (
) ;
(
)
4 (
)
4 (
) .
n
n
n
n
n
n
x L
x x b
b y y
b y y
a
x x b
b y y
b y y
a
Проведем замену координат:
1
1
1
2
2
1
1
1
2
1 2
1
;
2
2
;
2
.........................
2
;
2
;
;
....................
.
n
n
n
n
n
n
b y
w
b
b y y
w
b
b y y
w
b
v x
v x x
v x x
Проинтегрируем по
1
1
,..., ; ,...,
n
n
v v w w
и получим
(0)
3 2 1
2
2
0
2
2
1
( , , , ) 2
2
... 2
...
w
n n n
n
n
n
U
a L h a b L a b
w w w w dw dw
,


