Моделирование колебаний с инерционным возмущением
7
1 1
2
0
1
1
1
2
2
, 2
,
.
m l
m
l
c
l
K
n
h
M m m
M m m
M m m
⎛
⎞
+
ϕ ω
⎜
⎟
μ
⎝
⎠
=
=
=
+ +
+ +
+ +
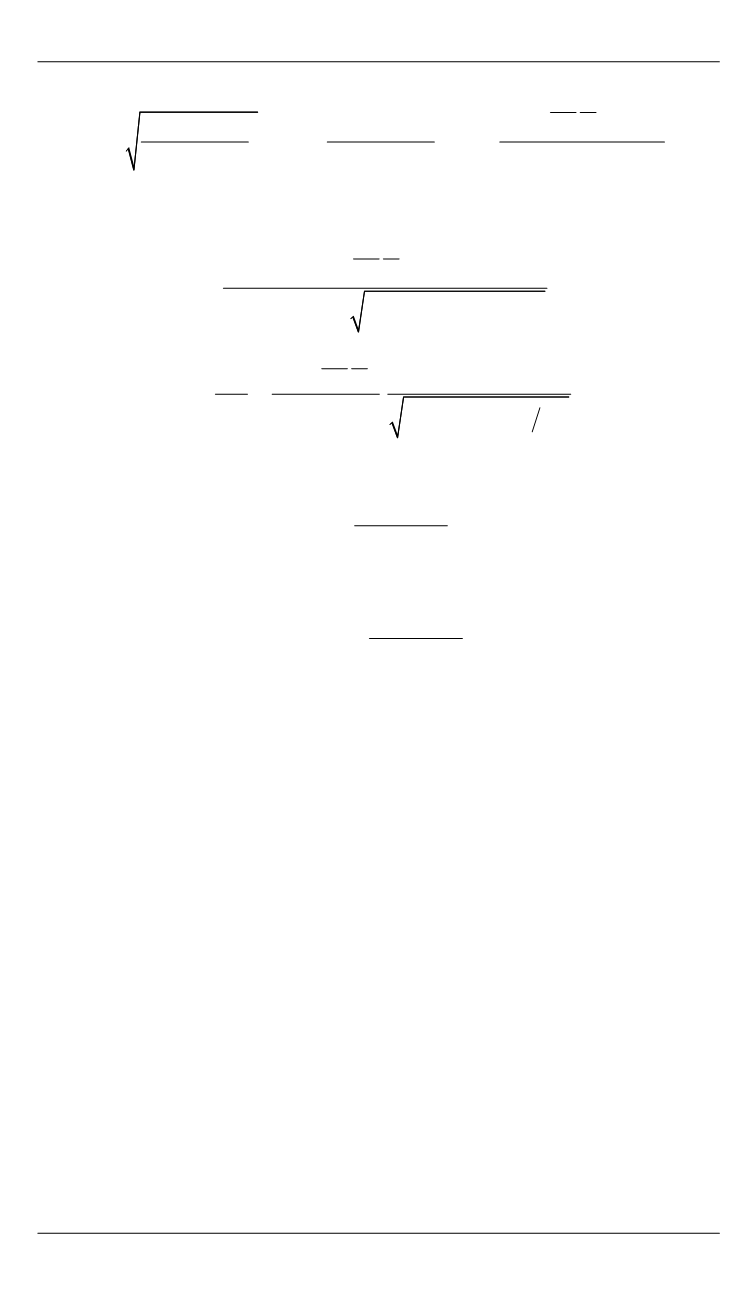
Таким образом, с учетом массы стержня получим
(
)
(
)
(
)
1 1
2
0
в
2
2
2
2 2
1
1 1
2
в
2 2
2 2
0
1
2
,
4
2
.
1
m l
m
l
l
a
M m m K
n
m l
m a
Z
l
l
M m m Z Z Q
⎛
⎞
+
ϕ ω
⎜
⎟
⎝
⎠
=
+ +
− ω + ω
+
λ = =
ϕ + +
− +
(5)
Для разности фаз
ε
имеем
(
)
2
tg
,
1
Z
Q Z
ε =
−
откуда
(
)
2
arctg
1
Z
Q Z
⎡
⎤
ε = ⎢
⎥
− ⎢
⎥
⎣
⎦
.
(6)
Методика проведения экспериментов.
Методику проведения в
данном лабораторном комплексе экспериментов по изучению вынуж-
денных колебаний механической системы с инерционным возмущени-
ем рассмотрим на конкретном примере. Пусть масса груза маятника
m
= 1,056 кг, масса тележки
M
= 5,557 кг (без дополнительных грузов
14 (см. рис. 2,
а
)). Приведенные ниже результаты испытаний получены
без дополнительных грузов и при длине маятника
l
= 0,196 м. По
результатам экспериментального замера жесткости пружин среднее
значение их коэффициента жесткости равно
c
ср
= 217,8 Н/м. Частота
свободных колебаний тележки с маятником, полученная расчетным
путем при этом значении
c
ср
,
K
≈
8,068 рад/с. Значения
K
, обусловлен-
ные разбросом измеренных величин жесткости
c
, лежат в диапазоне
K
≈
7,88 … 8,20 рад/с.
Непосредственно определить обобщенный коэффициент сопро-
тивления системы
n
(или
μ
) весьма трудно, поэтому найдем
n
с по-
мощью эксперимента. Чтобы оценить параметры
K
и
n
зарегистриру-
ем собственные затухающие колебания системы каретка — маятник.
Для этого отклоним систему (каретку с маятником) в крайнее допу-
стимое конструктивно положение и отпустим ее без начальной
скорости. Определим круговую частоту затухающих колебаний


