А.А. Панкратов
8
Характеристические показатели периодических решений, определяе-
мых условиями существования (5), (7), (18)–(21), образуют (при
1
3
S S
=
) четыре группы. 2S
2
-характеристических показателя (первая
группа) разлагаются в ряды по степеням
μ
, а остальные (три груп-
пы) — по целым степеням малого параметра
,
μ
причем разложения
показателей четвертой группы начинаются с членов порядка
2
:
μ
2S
2
-значений,
(0)
(1)
(2)
... ,
ε = ε μ + ε μ + ε μ μ +
2S
1
-значений,
(0)
(1) 2
(2) 3
... ,
η = η μ + η μ + η μ +
2(l – S
2
)-значений,
(0)
(1) 2
(2) 3
... ,
ν = ν μ + ν μ + ν μ +
2(N – 1 – S2)-значений
(0) 2
(1) 3
(2) 4
...
σ = σ μ + σ μ + σ μ +
Здесь
1 2 3
S , S , S
— размерность переменных J, , ,
ϕ ψ
входящих в
1
F
(в рассматриваемом случае
1
3
S S ),
=
коэффициенты
(0)
,
ε
(0)
,
η
(0)
,
ν
(0)
σ
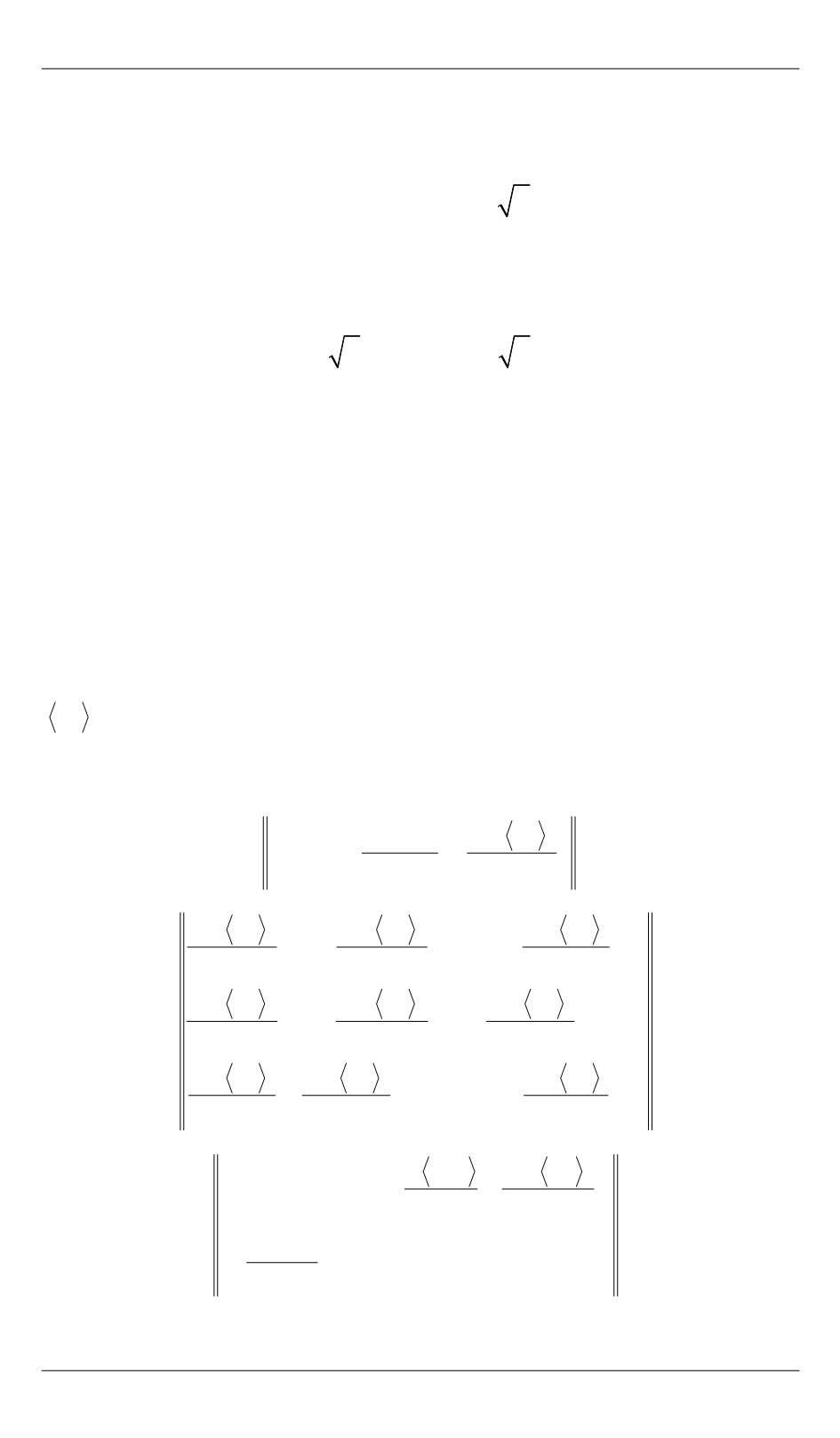
являются решениями следующих алгебраических уравне-
ний:
2
2
2
1
0
2
т
т
1 1
11 11
det E
0,
S
F
F
a a
∂⎛
⎞
∂⎛
⎞
ε +
=
⎜
⎟
⎜
⎟ ′ ′
∂ ∂
∂ω ∂ω
⎝
⎠ ⎝
⎠
(22)
1
1
2
2
2
1
1
1
т
т
т
11 11
21 11
21 11
2
2
2
1
1
1
т
т
т
11 21
21 21
21 21
2
2
2
1
1
1
т
т
т
11 21
21 21
21 21
det
E 0,
E
S
S
F
F
F
a
F
F
F
a
F
F
F
a
a
a a
∂
∂
∂
∂ω ∂ω ∂ω ∂ω
∂ ∂ω
∂
∂
∂
− η =
∂ω ∂ω ∂ω ∂ω ∂ ∂ω
∂
∂
∂
+ η
∂ω ∂ ∂ω ∂
∂ ∂
(23)
2
2
2
I2
2
т
12
12 12
2
0
т
1 1
0 E
det
0,
0
E
l S
l S
F
F
a a
−
−
∂ Φ ∂
−ν
+
∂ω ∂ω ∂ω
=
∂
ν
∂ ∂
(24)


