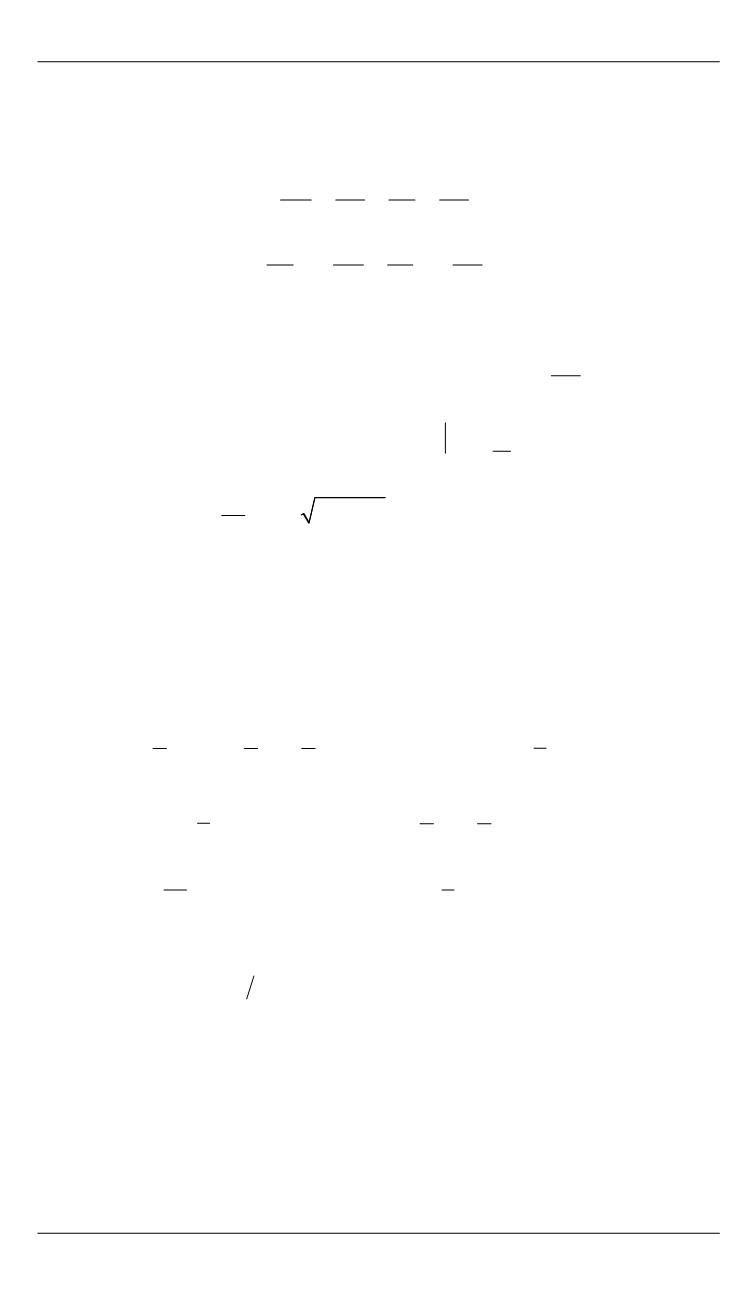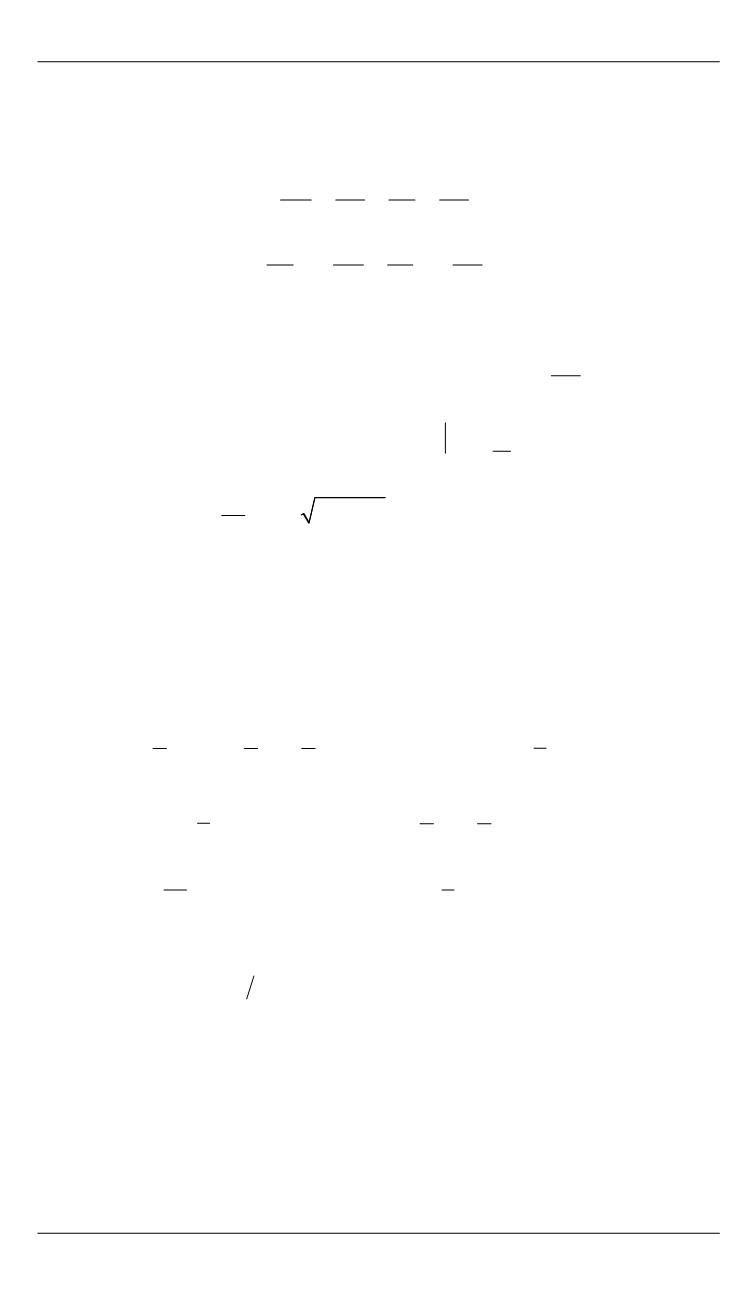
А.А. Панкратов
10
ровой круговой орбите, уравнения движения спутника с использова-
нием интегралла Якоби были приведены к так называемой форме
уравнений Уиттекера:
,
,
g
,
,
dG F dL F
dh
dh l
dg F dl
F
dh G dh L
∂
∂
=
=
∂
∂
∂
∂
= −
= −
∂
∂
(27)
где
(
)
2
2
0
1
2
0
1
, , , ,
,
;
2
G
F F F L G l g h F
F
C
= + μ
+ μ +
= −
…
(
)
2
0
1
1
1
2
, , , , ,
,
G H F
C
F F L G H l g h
= = −
=
(28)
(
)
1 2
1 2
2
2
2
1
0
,
1
2
,
sin cos
cos
2
( , ) cos(
).
k k
k k
L F
G L
l L
U
k g k h
= − χ
− β + β −
−
ρ ϑ
+
∑
Здесь суммирование проводится по индексам
1
0, 1, 2;
k
=
2
0, 2,
k
= ±
а коэффициенты разложения
1 2
,
( , )
k k
U
ρ ϑ
определяются
следующими формулами:
2
2
2
0.0
3
3 3
sin
1 sin sin ,
4
4 2
U
⎛
⎞
= ϑ + − ϑ ρ
⎜
⎟
⎝
⎠
2
2
2.0
3 sin sin ,
8
U
= − ϑ ρ
1.0
3 sin 2 sin 2 ,
8
U
= ρ ϑ
2
2
0.2
3 3 1 sin sin ,
4 2
U
⎛
⎞
= − − ϑ ρ
⎜
⎟
⎝
⎠
(29)
2
2
2. 2
3 sin (1 cos ) ,
16
U
±
= −
ϑ ± ρ
1. 2
3 sin 2 sin (1 cos ).
8
U
±
=
ϑ ρ ± ρ
∓
В качестве малого параметра было выбрано динамическое сжатие
спутника
(
) ,
A C A
μ = −
где
, ,
A B C
(
)
A B
=
— главные централь-
ные моменты инерции спутника.
При значении
0
μ =
уравнения (27)–(29) легко интегрируются:
0
,
G G
=
0
,
L L
=
0
0
,
g G h g
= − +
0
.
l l
=
(30)
Здесь
0 0 0 0
,
,
,
G L g h
— постоянные интегрирования. При рациональ-
ном
0
G
решение (30) будет периодическим. Рациональность
0
G
означает соизмеримость между невозмущенным значением угловой