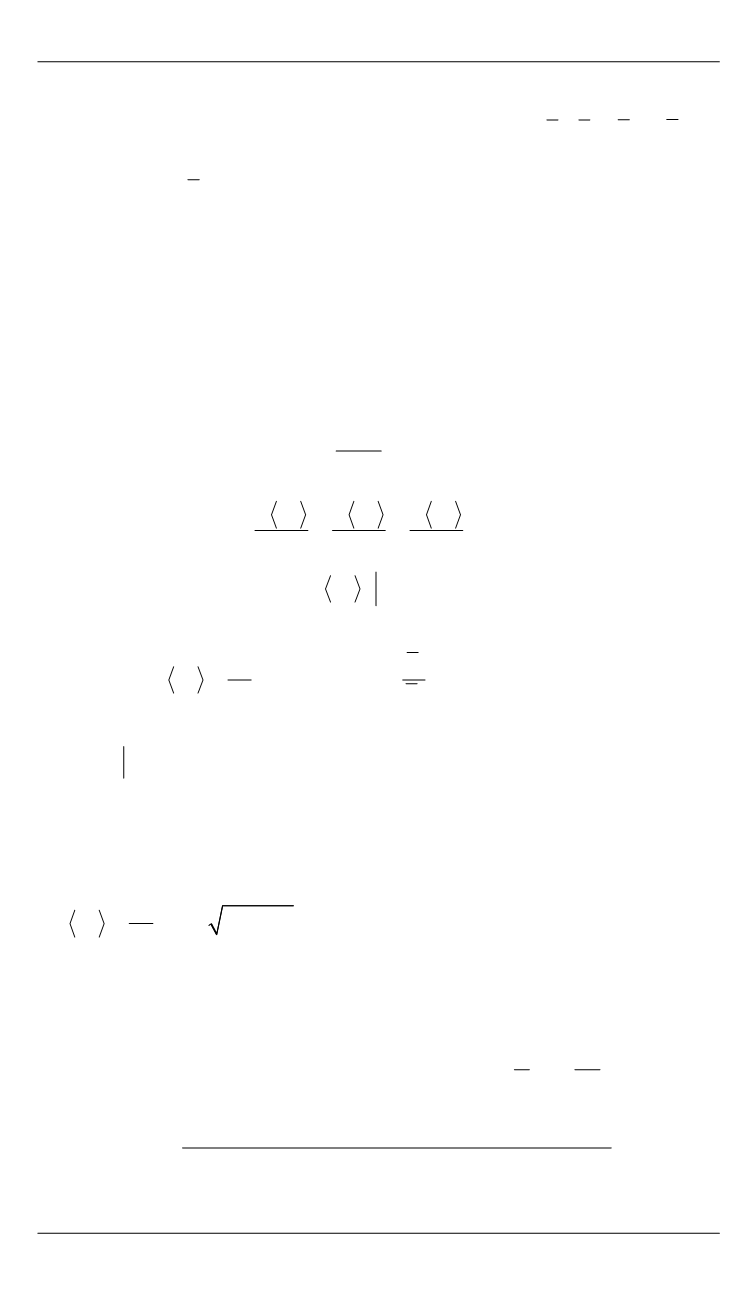
Устойчивость периодических движений осесимметричного спутника…
11
скорости вращательного движения спутника-гиростата
( )
0
n
и сред-
ним орбитальным движением
,
ω
т. е.
( )
0
0
1 2
:
:
G n
k k
= ω =
1
(
k
и
2
k
—
взаимно простые целые числа). Период такого решения (по перемен-
ной
)
h
0
2
2 .
T k
= π
При исследовании вопроса о существовании периодических ре-
шений системы (27) при
0
μ ≠
использовали достаточные условия,
сформулированные в теоремах 1, 2.
Система (27) допускает при малых
0
μ ≠
голоморфные по малому
параметру
μ
T
0
-периодические решения, близкие к порождающему
решению (решение (30) при
0
1
G
= ±
), если параметры порождающе-
го решения удовлетворяют условиям:
2
0
2
0
0,
F
G
∂
≠
∂
(31)
1
1
1
0
0
0
0,
F F F
l
g
L
∂
∂
∂
=
=
=
∂
∂
∂
(32)
(
)
0 0 0
1
,
,
Hes
0,
l
g L
F
≠
(33)
где
0
T
1
1
1 0
0
0 0
0
2
0
1
,
,
, ,
;
T
k
F
F L G h g l h dh
k
⎛
⎞
=
− +
⎜
⎟
⎝
⎠
∫
(34)
( )
,
Hes
x y
Φ
— определитель Гессе, вычисленный от функции
Φ
по
величинам, стоящим справа от вертикальной черты.
Вычисляя интеграл (42), получаем
для
0
1
G
= ±
( )
(
)
0
:
1: 1 :
n
ω = ±
{
}
2
0
2
2
1
0
0
0
0
0
0,0
2, 2
0
sin cos
cos
cos 2 .
2
L F
G L
l L
u u
g
±
= − χ
− β + β − −
(35)
Условие (31) выполняется при любом значении
0
.
G
Подставляя выражение (35) в уравнение (32), находим следую-
щие решения:
1)
0 0
,
ρ θ
и
β
произвольны;
0
0
3
0, ;
0,
, ,
;
2 2
l
g
π π
= π =
π
(
)
(
)
2
0
0
0
0
0
1
sin 2 3 6 cos
6 cos 2 3
;
16sin
ε θ − σ ρ − εσ θ + − σ
⎡
⎤
⎣
⎦
χ =
θ − σ β