Устойчивость периодических движений осесимметричного спутника…
3
для одного особого (важного для приложений) случая были найдены
новые достаточные условия существования периодических решений;
изучена структура разложения характеристических показателей в ря-
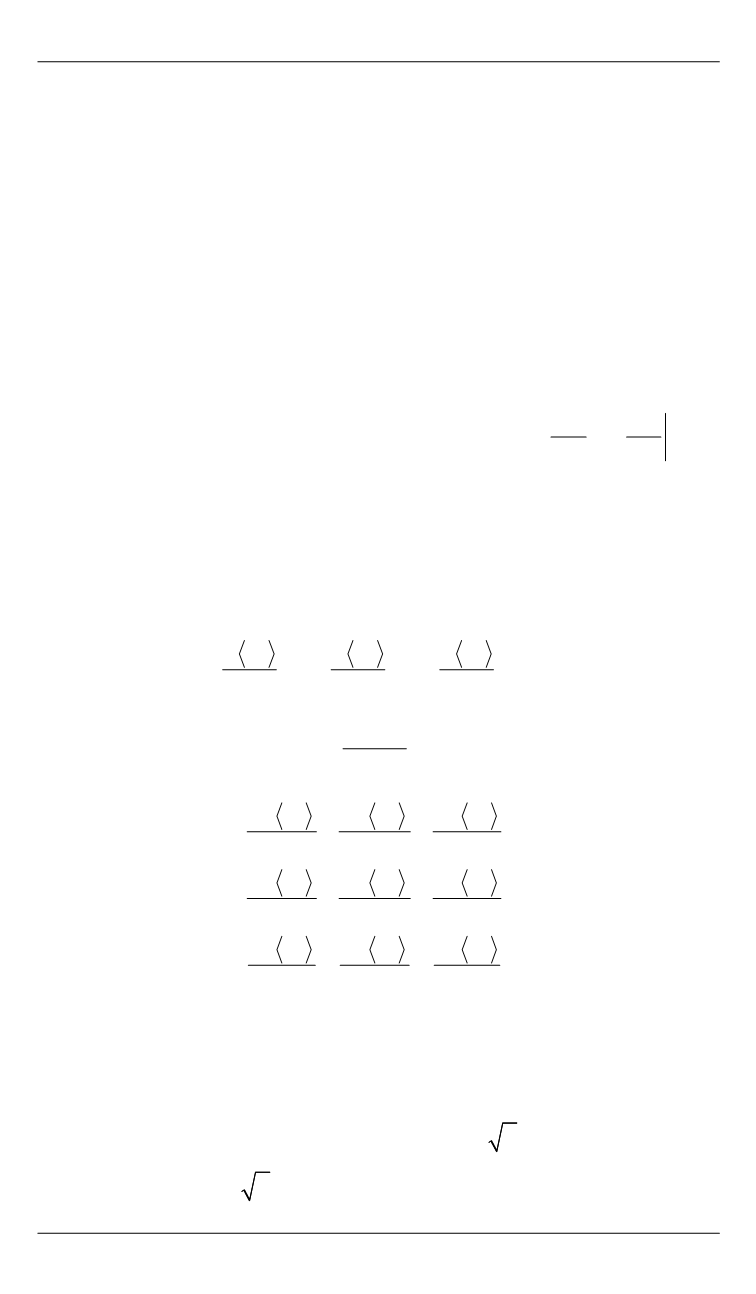
ды по целым и дробным степеням малого параметра
μ
и получены
алгебраические формулы для нахождения основных коэффициентов
в разложениях соответствующих характеристических показателей.
Сформулируем соответствующие результаты в виде теорем.
Теорема 1.
Дифференциальные уравнения (1)–(3) допускают при
малых
0
μ ≠
периодические решения, близкие к порождающему ре-
шению
1
I
,
а
=
2
J
,
а
=
(0)
1
,
n t
ϕ = + ω
2
ψ = ω
(4)
(
1 2
1
2
,
,
,
а a
ω ω
— некоторые постоянные;
1 1
0
0
(0)
т
т I
1
1
),
I
a
F F
n
a
=
∂
∂
= − = −
∂
∂
если параметры
1 2
1
2
,
,
,
а a
ω ω
порождающего решения удовлетво-
ряют следующим условиям:
(
)
(0) т
1 2
1
1 2
1
( ) ,
c( , , ..., ,
),
с 0,
Z, НОД ( , , ..., ,
) 1,
l
N
i
l
N
n
k k
k k
k
k k
k k
+
+
Ω =
≠ ∈
=
(5)
1
т
1
0,
F
∂
=
∂ω
1
т
2
0,
F
∂
=
∂ω
1
т
2
0,
F
a
∂
=
∂
(6)
2
0
т
1 1
det
0,
F
a a
∂⎛
⎞ ≠
⎜
⎟
∂ ∂ ⎝
⎠
(7)
2
2
2
1
1
1
т
т
т
1 1
2 1
2 1
2
2
2
1
1
1
т
т
т
1 2
2 2
2 2
2
2
2
1
1
1
т
т
т
1 2
2 2
2 2
det
0.
F
F
F
a
F
F
F
a
F
F
F
a
a a a
∂
∂
∂
⎛
⎞
⎜
⎟
∂ω ∂ω ∂ω ∂ω ∂ ∂ω
⎜
⎟
⎜
⎟
∂
∂
∂
≠
⎜
⎟
∂ω ∂ω ∂ω ∂ω ∂ ∂ω
⎜
⎟
⎜
⎟
∂
∂
∂
⎜
⎟
∂ω ∂ ∂ω ∂ ∂ ∂
⎝
⎠
(8)
Характеристические показатели этих периодических решений
будут двух типов (считаем, что уравнения, определяющие основные
коэффициенты в разложениях характеристических показателей име-
ют простые корни): первый тип характеристических показателей
(2
l
-значений) разлагается в ряды по степеням
:
μ
(0)
(1)
(2) 3/2
... ,
i
i
i
i
ε = ε μ + ε μ + ε μ +
1, 2, ..., ,
i
l
=
(9)


