Обзор моделей нестационарного качения колеса с упругой шиной…
9
Альтернативой является кинематическая гипотеза Келдыша –
Уайли [3, 4]. Отсутствие скольжения пневматика он ставит в соответ-
ствие следующим двум условиям:
1) касательная к линии качения пневматика совпадает с осью по-
верхности контакта;
2) кривизна линии качения пневматика однозначно определяется
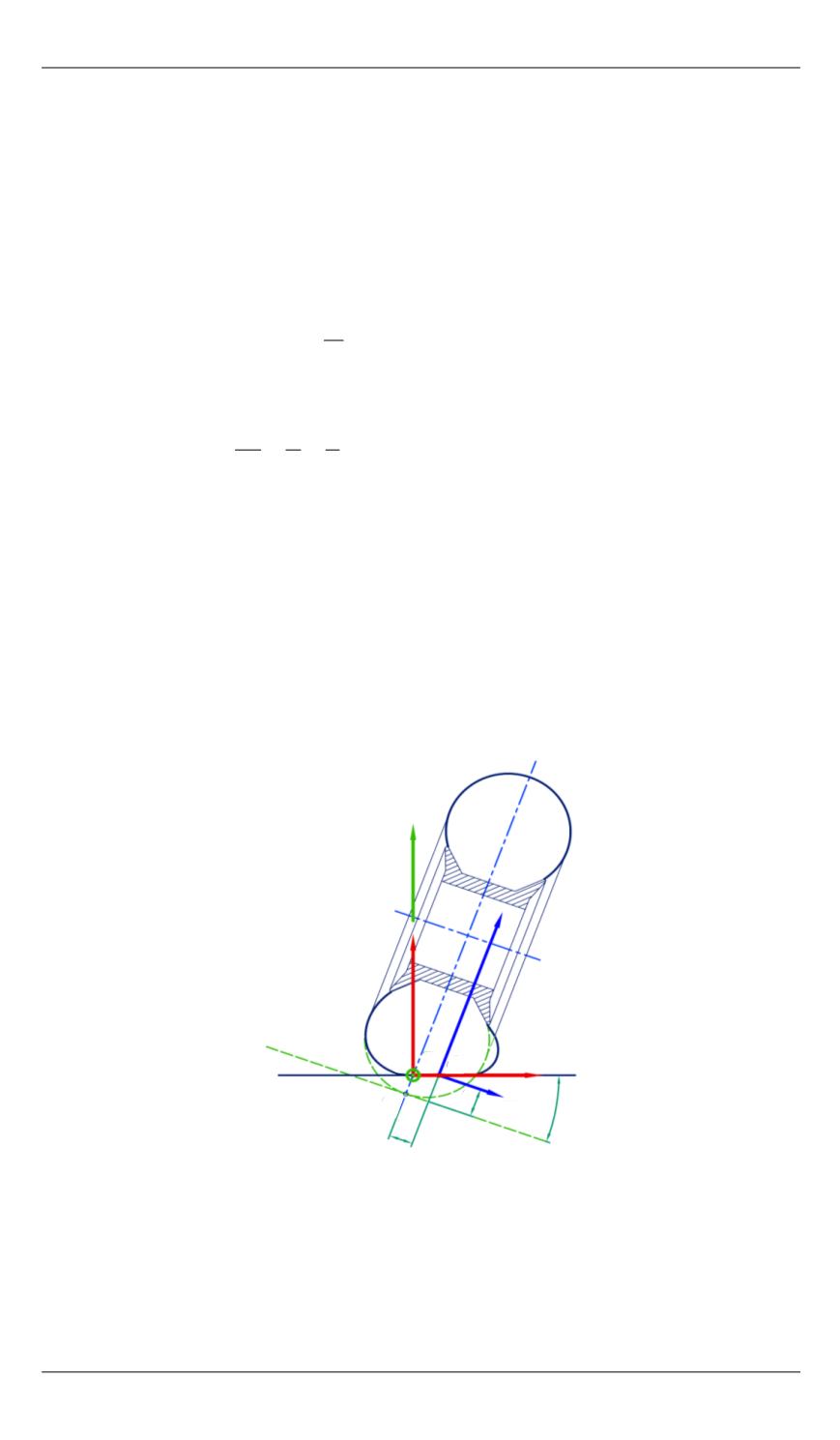
тремя параметрами деформации шины (рис. 9):
1
A B C
R
= λ − ϕ− χ
,
где
R
— радиус кривизны траектории качения пневматика;
[
]
2
2 2 1
A B C
r r r
⎡
⎤
= ⎢
⎥
⎣
⎦
— постоянные коэффициенты, опреде-
ляемые эмпирическими функциями от радиуса колеса
r
;
λ
— рас-
стояние от линии пересечения диаметральной плоскости смещенного
обода колеса с опорной плоскостью до центра площади контакта на
исходной поверхности (аналог поперечного смещения);
ϕ
— угол,
отсчитываемый от той же линии до средней линии пятна контакта до
деформации (аналог угла увода);
χ
— угол между диаметральной
плоскостью смещенного обода и вертикальной осью (аналог угла
развала).
h
λ
1
O
A
O
L
F
1
F
χ
N
M
P
Рис. 9.
Схема деформации шины
Этот подход успешно применялся для решения практических
проблем шимми в авиации, однако экспериментальные данные пока-
зали, что коэффициенты не являются инвариантными по отношению
к системе сил. Таким образом, при простой реализации учета неста-


