П.И. Саркисов, С.Д. Попов
10
ционарного режима и угла наклона плоскости вращения колеса, мо-
дель малопригодна для решения задач автомобилестроения в силу
отсутствия скольжения, зависимости от системы сил и невозможно-
сти учета продольных силовых факторов.
Принципиально иной подход к моделированию поведения упру-
гого тела шины — описание кинематических связей, наложенных на
тело. Этот подход свободен от гипотез, т.
е. не является заведомо
противоречивым, однако характеризуется более сложной формой
дифференциальных уравнений движения, требующей применения
специальных методов для их решения.
Примером такого подхода является описание, предложенное
И.И. Метелицыным [6, 7], согласно которому беговая дорожка шины
представлена деформируемым тором с условно-точечным контактом
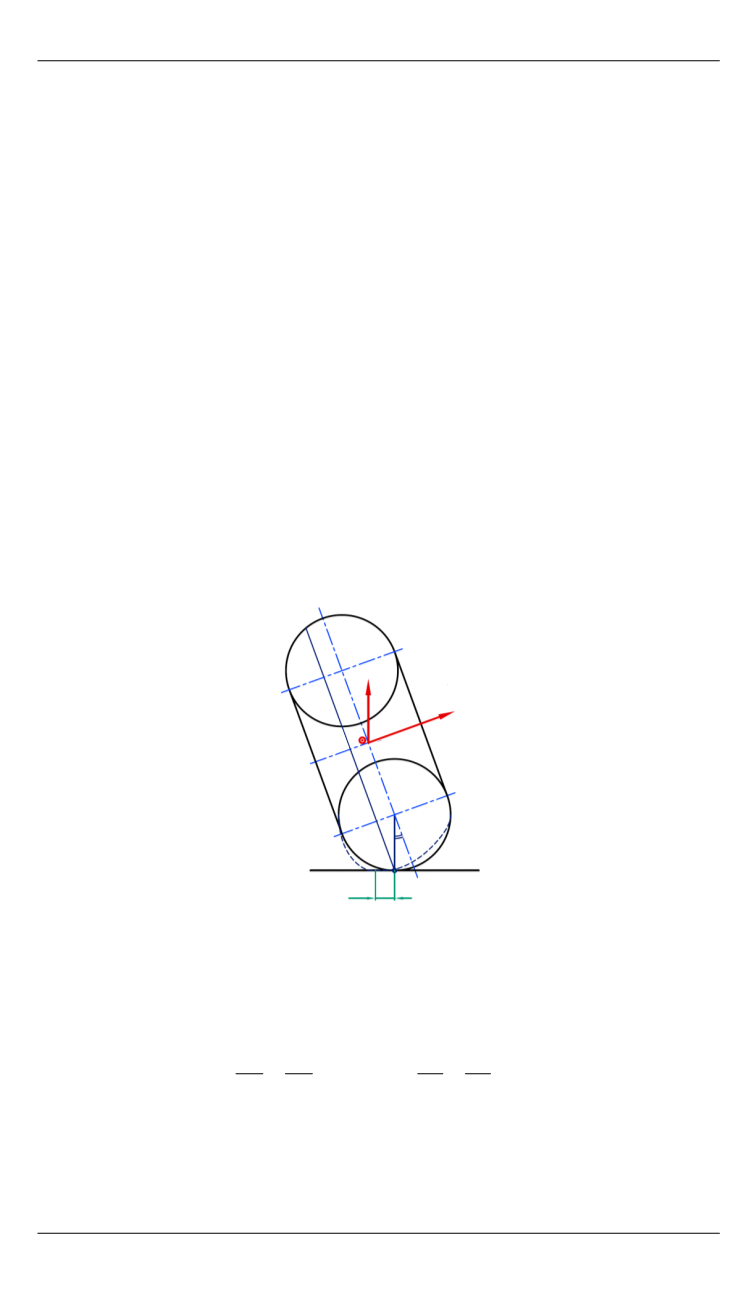
без скольжения (рис. 10). Это означает, что силовые факторы прило-
жены в точке, но в контакте с опорным основанием находится не
только точка, но и бесконечно малая ее окрестность, т.
е. точки этой
окрестности также имеют нулевую абсолютную скорость. В точке
контакта отсчитываются две координаты деформации — поперечное
линейное смещение и скручивание вокруг вертикальной оси.
u
θ
&
θ
&
ψ
&
ϕ
Рис. 10.
Координаты движения шины
Касание тора и плоскости определяется геометрическим услови-
ем наличия общей нормали
0;
0
⎛
⎞
∂ ∂
∂ ∂
⎛
⎞ + =
+ =
⎜
⎟
⎜
⎟
∂α ∂α
∂β ∂β
⎝
⎠
⎝
⎠
u
u
n
n
ρ
ρ
,
(5)
где
n
— вектор нормали к опорной поверхности;
ρ
— радиус-вектор
точки тора относительно его центра;
u
— вектор поперечного сме-
щения точки контакта шины (в плоскости опорного основания);


