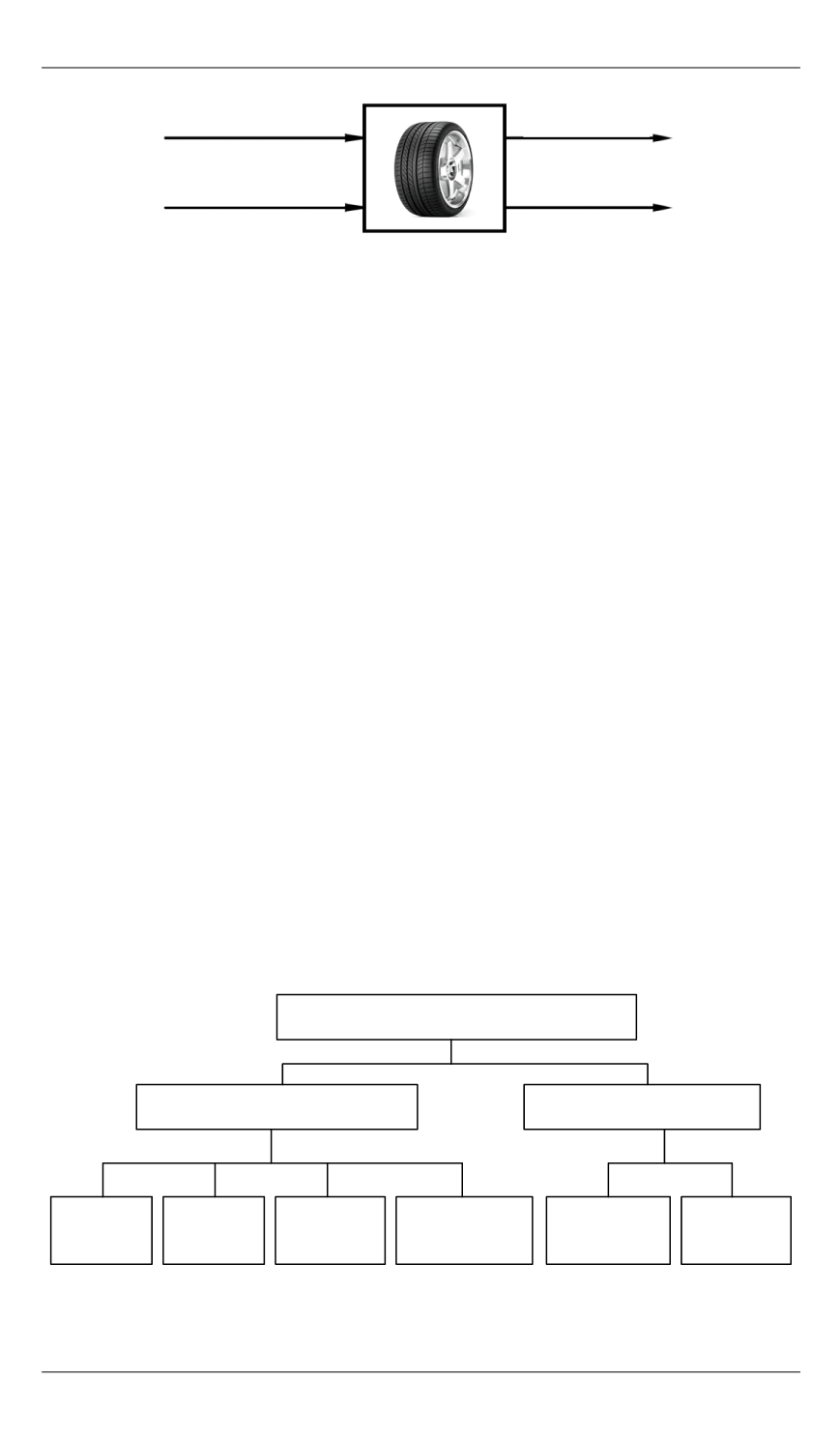
Обзор моделей нестационарного качения колеса с упругой шиной…
3
( ) ( ) ( )
x t y t z t
( ) ( ) ( )
t
t
t
ϕ ψ θ
( )
x
F t
( )
y
F t
( )
z
M t
Рис. 2.
Схема передаточной функции шины (черный ящик)
На сегодняшний день предложено множество подходов к моде-
лированию качения шины при плоском движении центра колеса.
В большинстве из них используется какая-либо гипотеза для описа-
ния поведения шины. Ж. Брулье (1925, [1]) в качестве такой гипотезы
использовал линейную зависимость боковой реакции в площадке
контакта от угла увода. Х. Пажек (1966, [2]) впервые предлагает эм-
пирическую формулу нелинейной связи боковой реакции с углом
увода. Академик М.В. Келдыш гипотетически связал кривизну траек-
тории следа качения колеса с тремя кинематическими параметрами
деформации пневматика (1945, [3, 4]). К другому типу гипотез отно-
сится (очень многочисленная группа) аппроксимация шины каким-
либо механическим аналогом с соответствующими связями, подда-
ющимся описанию уравнениями состояния [5].
Отметим, что описание с помощью гипотез принципиально не-
корректно, так как избыточно по отношению к механике, однако су-
щественно упрощает решение частных задач. Альтернативный класс
подходов (рис. 3) — описание кинематических связей, наложенных
на движение точек внешней поверхности шины — принципиально
корректный, поскольку не накладывает никаких связей, не имеющих
места в действительности. К этой группе принято относить подходы,
предложенные И.И. Метелицыным (1952, [6, 7]) и В.С. Гоздеком
(1970, [8, 9]).
Плоское движение центра колеса
Описание на основе гипотезы
Описание системы связей
Подход
Брулее
Подход
Пажека
Подход
Келдыша
Механические
аналоги
Подход
Метелицына
Подход
Гоздека
Рис. 3.
Классификация основных подходов к моделированию качения
колеса без его возмущения по вертикальной оси


