П.И. Саркисов, С.Д. Попов
4
Примером моделей на основе механического аналога является
нить на упругом основании, где тело шины заменяется замкнутой
растяжимой нитью без изгибной жесткости, лежащей на цилиндре
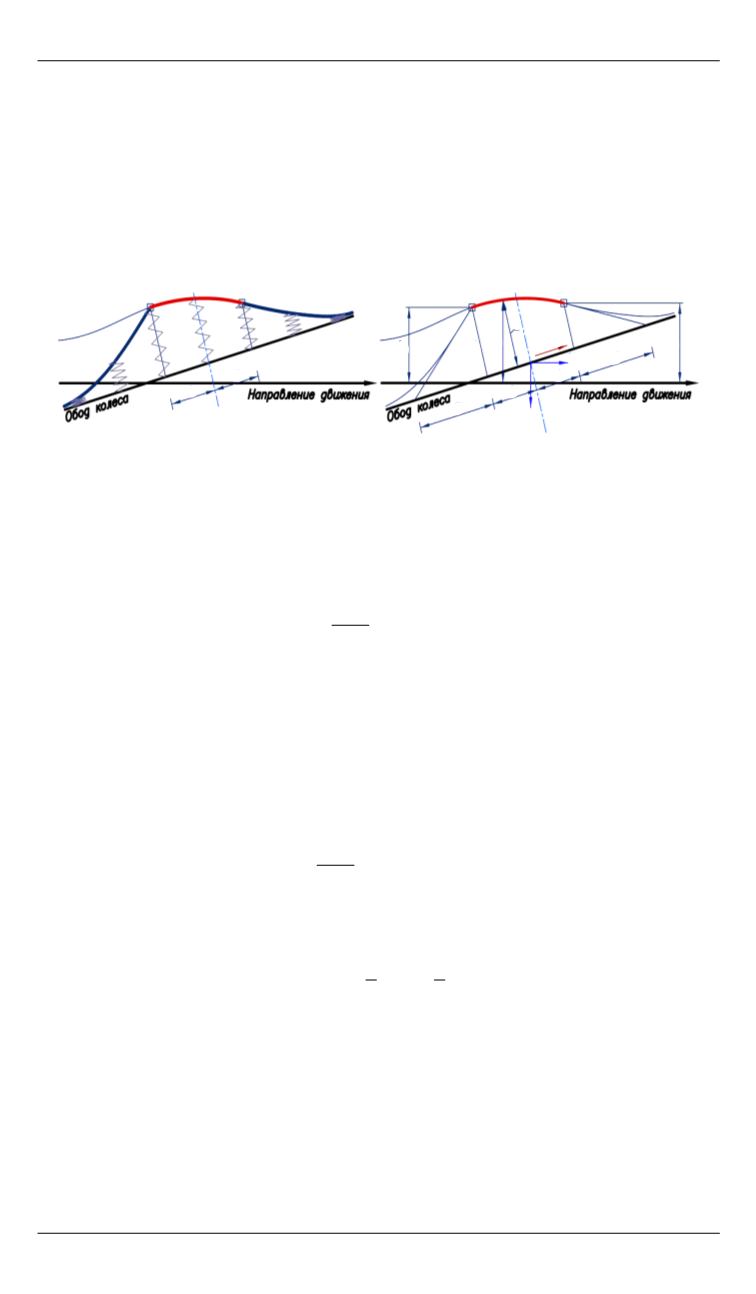
постоянного радиуса и плоскости площадки контакта. Каждая точка
нити упруго связана с абсолютно жестким диском (рис. 4) [5]. Уча-
сток нити, лежащий в площадке контакта, неподвижен относительно
поверхности земли, т.
е. в модели не предусмотрено скольжение.
l
l
2
h
2
q
σ
h
q
l
y
l
x
s
1
q
σ
1
h
Рис. 4.
Схемы модели типа нити на упругом основании
Деформированное состояние нити описывается двумя дифферен-
циальными уравнениями изогнутой оси балки:
• для свободного участка
2
2
0,
d q T
kq
ds
− + =
(1)
где
T
— сила натяжения нити, т. е. сила натяжения коронной части ши-
ны;
( )
q s
— боковое перемещение коронной части шины относительно
обода колеса;
s
— координата, измеряемая вдоль коронной части шины;
k
—жесткость упругого основания (боковая жесткость шины);
• для контактной площадки, где добавляются распределенные бо-
ковые силы трения на нити
( )
p s
:
2
2
( )
d q T
kq p s
ds
− + =
.
(2)
Решением уравнения (1) является экспоненциальный закон ре-
лаксации свободной части нити:
s
s
q Ae Be
−
σ
σ
= +
.
Здесь
,
A B
— константы, определяемые из граничных условий;
σ
—
длина подкасательной экспоненциальной кривой, называемая длиной
релаксации.
Решением уравнения (2) является уравнение кривой для нити в
площадке контакта.
При переходе к нестационарному режиму используют условие
отсутствия скольжения, выражающееся в связи формы нити в кон-


