П.И. Саркисов, С.Д. Попов
6
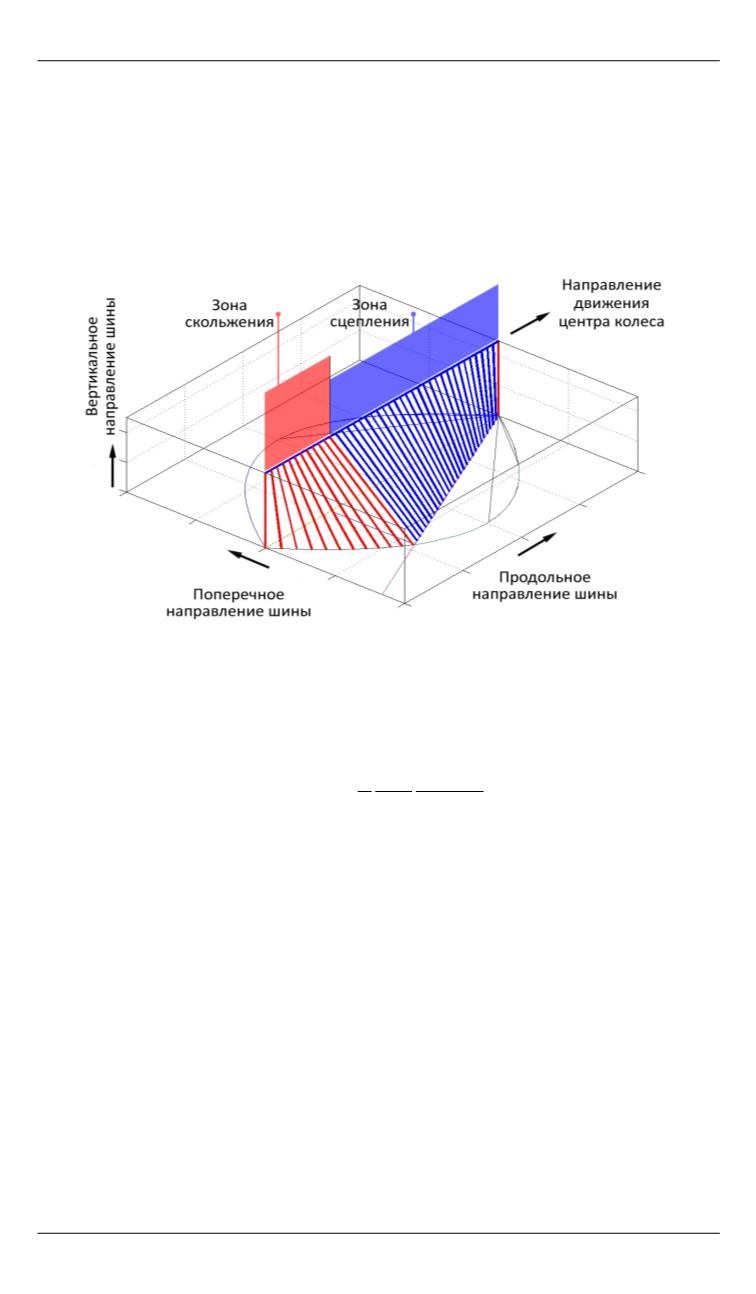
Распределение вертикальной реакции по длине контакта может
быть задано произвольным законом, для простоты принимают пара-
болическую эпюру [2]. Описание трения также может быть реализо-
вано различными моделями, в самом примитивном случае это сухое
трение, тогда граница по сцеплению элементарной боковой силы
также будет параболой (рис. 6).
z
y
x
Рис. 6.
Моделирование щеточной структуры при движении с уводом
Параболическая граница перемещения элемента соответствует
пределу сцепных свойств:
2 2
max
3
3 ( )
4
z
y
F a x
v x
c a
μ −
=
,
где
max
( )
v x
— максимальное поперечное отклонение элемента, при
котором отсутствует скольжение;
μ
— коэффициент трения сколь-
жения;
z
F
— результирующая сила вертикальной реакции шины;
a
— половина длины отрезка контакта;
x
— продольная координата
шины, отсчитываемая от центра контакта в направлении движения
колеса;
y
c
— жесткость упругого элемента в поперечном относи-
тельно шины направлении.
Площадка контакта делится на две зоны. В первой зоне сила
упругости, воспринимаемая отклонившимися элементами, не исчер-
пывает всех возможностей элемента по сцеплению, и они не скользят
относительно опорного основания. Во второй зоне сила упругости
растет и превышает предел по сцеплению, и элемент начинает сколь-
зить под действием уже постоянной силы трения скольжения.


