П.И. Саркисов, С.Д. Попов
12
странственного возмущенного качения упругого колеса по твердой
плоскости. Он рассматривал движение как совокупность невозму-
щенного (прямолинейного с постоянной скоростью
V
) и возмущен-
ного (отклонения от первого) движений. Такая модель содержит ряд
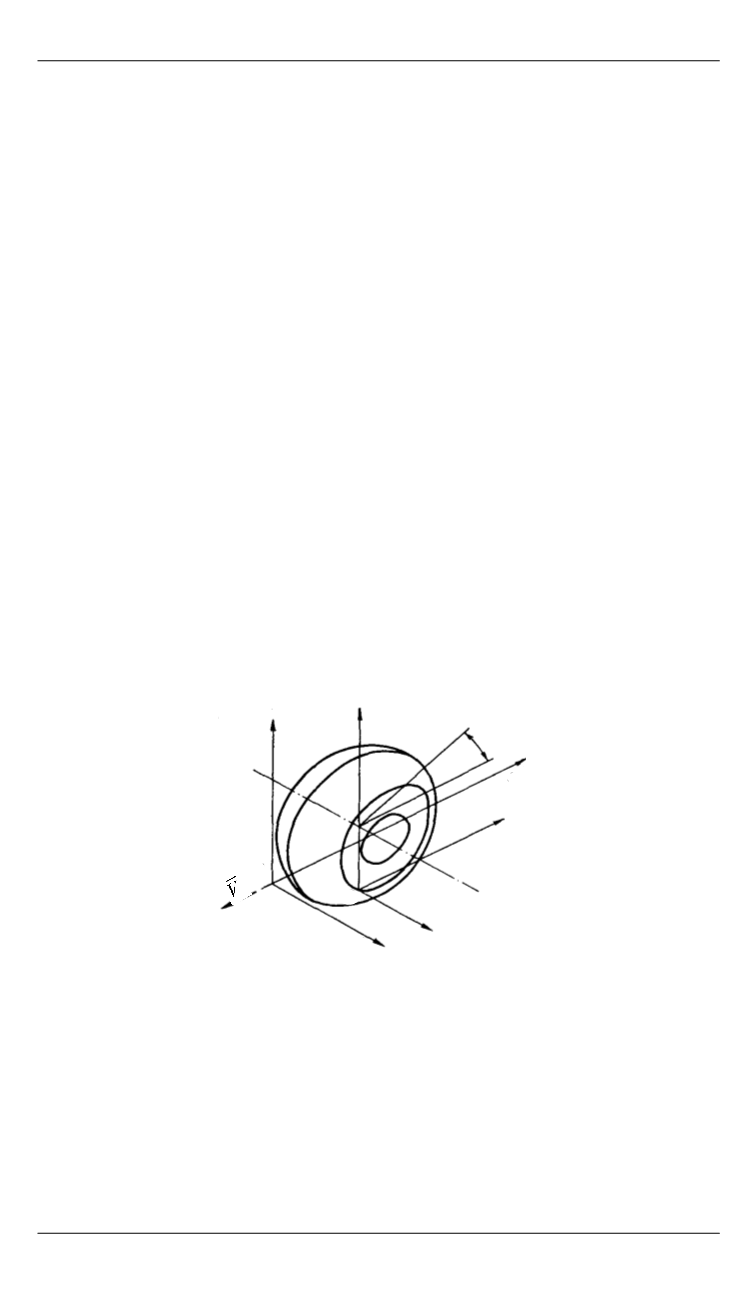
систем координат (рис. 11) и описывает радиус-вектор точки дефор-
мированной поверхности пневматика в абсолютной системе как век-
торную сумму радиус-векторов этой точки в каждой из вложенных
систем координат, связанных с деформацией, вращением и переме-
щением пневматика. Гоздек вводит движущуюся со скоростью
V
систему координат
О x y z
′ ′ ′ ′
, ось
О x
′ ′
которой находится на поверх-
ности земли и направлена против вектора скорости
V
, а ось
О y
′ ′
перпендикулярна поверхности земли. Кроме того, он вводит систему
координат
Оxyz
, оси
Оx
и
Оy
которой лежат в плоскости симмет-
рии колеса. При этом ось
Оx
параллельна поверхности земли, а
центр колеса находится на оси
Оy
на неизменном расстоянии от
начала координат. При невозмущенном движении системы коорди-
нат совпадают. Тогда возмущенное движение корпуса колеса опреде-
ляется смещениями ( ), ( ), ( )
x
y
z
s t s t s t
точки
O
в направлении осей
,
,
О x О y О z
′ ′
′ ′
′ ′
, углами поворота
( ), ( )
x
y
t
t
ϕ ϕ
системы координат
Оxyz
относительно осей
О x
′ ′
и
О y
′ ′
, а также приращением
( )
z
t
ω
угловой скорости корпуса колеса относительно оси его вращения.
O
′
y
′
y
θ
x
′
x
z
z
′
O
Рис. 11.
Вспомогательные системы координат шины
Смещение
( , , , )
x y z t
r
Δ
точек поверхности шины, обусловленное
возмущенным движением (относительно той же точки поверхности
шины, совершающей невозмущенное движение), выражается в век-
торной форме для базиса, ориентированного по осям
,
,
Оx Оy Оz
:
( , , , ) ( , , , )
( , , , )
( , , , )
x y z t u x y z t i v x y z t j w x y z t k
Δ
=
+
+
r
r
r
r
,


