Фазовые скорости бегущих волн в цилиндрической оболочке при конечной и бесконечной …
7
Кирхгофа – Лява найдем решение второго уравнения в виде гармо-
нической функции
2
,
cos
w
w s t
B s
t
. Из второго уравнения
системы (7), разделив на
w
, получим следующее уравнение:
4
2
11
22
1
0
w
rD
C
r h
r
.
(12)
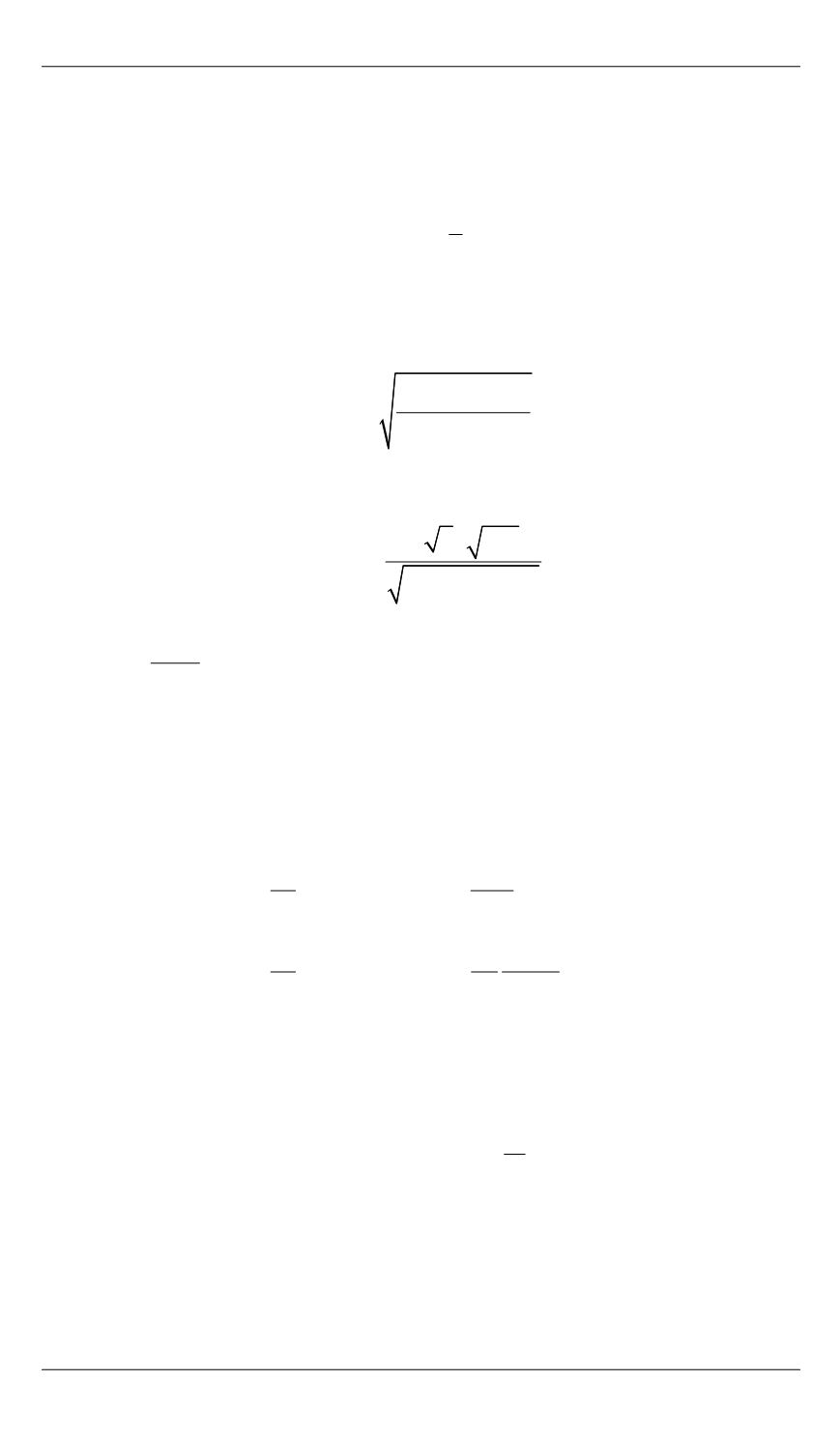
Для нахождения скорости волны изгиба выразим из уравнения
(12)
:
w
2 2
22
4
2
11
ω ρ
φ
r
h C
w r D
.
(13)
Разделим частоту на φ
w
, получим
4
11
К Л 2
2
4
22
,
r D
a
r h C
(14)
где
3
1
11
22
2
;
.
12
E h
D
C E h
Выражение (14) дает точное значение фазовой скорости волны
изгиба в принятых допущениях в случае гипотезы Кирхгофа – Лява.
Рассчитаем фазовую скорость изгибной волны в случае принятия
гипотезы Тимошенко. Для расчета вынужденных изгибных колеба-
ний используем два последних уравнения системы (8):
2
2
2 3
2
0,
0,
12
s
s
s
w
rQ N r h
s
t
h s
rM rQ r
s
t
(15)
с граничными условиями
0,
0,
w t
0,
0,
s
t
,
0,
s
M L t
,
cos .
s
Q L t
J
t
Найдем решение системы в виде
Т
1
2
,
s
i t
a
s
C w
e
C
(16)
где
1 2
,
C C
– произвольные константы;
– частота возмущающей
силы;
Т
a
– фазовая скорость бегущей волны в случае принятия гипо-
тезы Тимошенко.


