Фазовые скорости бегущих волн в цилиндрической оболочке при конечной и бесконечной …
11
Из рисунка ясно, что независимо от частоты, начиная с опреде-
ленного значения жесткости поперечного сдвига, скорости волн из-
гиба стремятся к предельному значению.
Найдем предельное значение фазовой скорости изгибной волны
из уравнения (18) при
1
:
K
4
11
2
2
3
4 2
3
2 2
22
11
11
.
24
24
r D
a
r h
r h
r h C
D
D
(24)
Сравним полученный результат со скоростью изгибной волны
при использовании гипотезы Кирхгофа – Лява (14), для чего найдем
разность предельной фазовой скорости в оболочке Тимошенко (24) и
фазовой скорости в оболочке Кирхгофа – Лява (14):
2 2
4
22
К Л К Л
2
2 2
22
1 ,
r h C
a a a
r h C
(25)
где
2
3
11
24
r h
D
.
Прежде всего отметим, что действительная фазовая скорость по-
лучается при неотрицательном
2
2
22
,
r h C
т. е. когда круговая ча-
стота вынужденных колебаний больше отношения скорости про-
дольной волны в окружном направлении к радиусу оболочки. При
этом условии корень в знаменателе имеет одно действительное и од-
но мнимое значение. Рассматривая только действительное значение,
проведем замену:
2
2
22
.
r h C
(26)
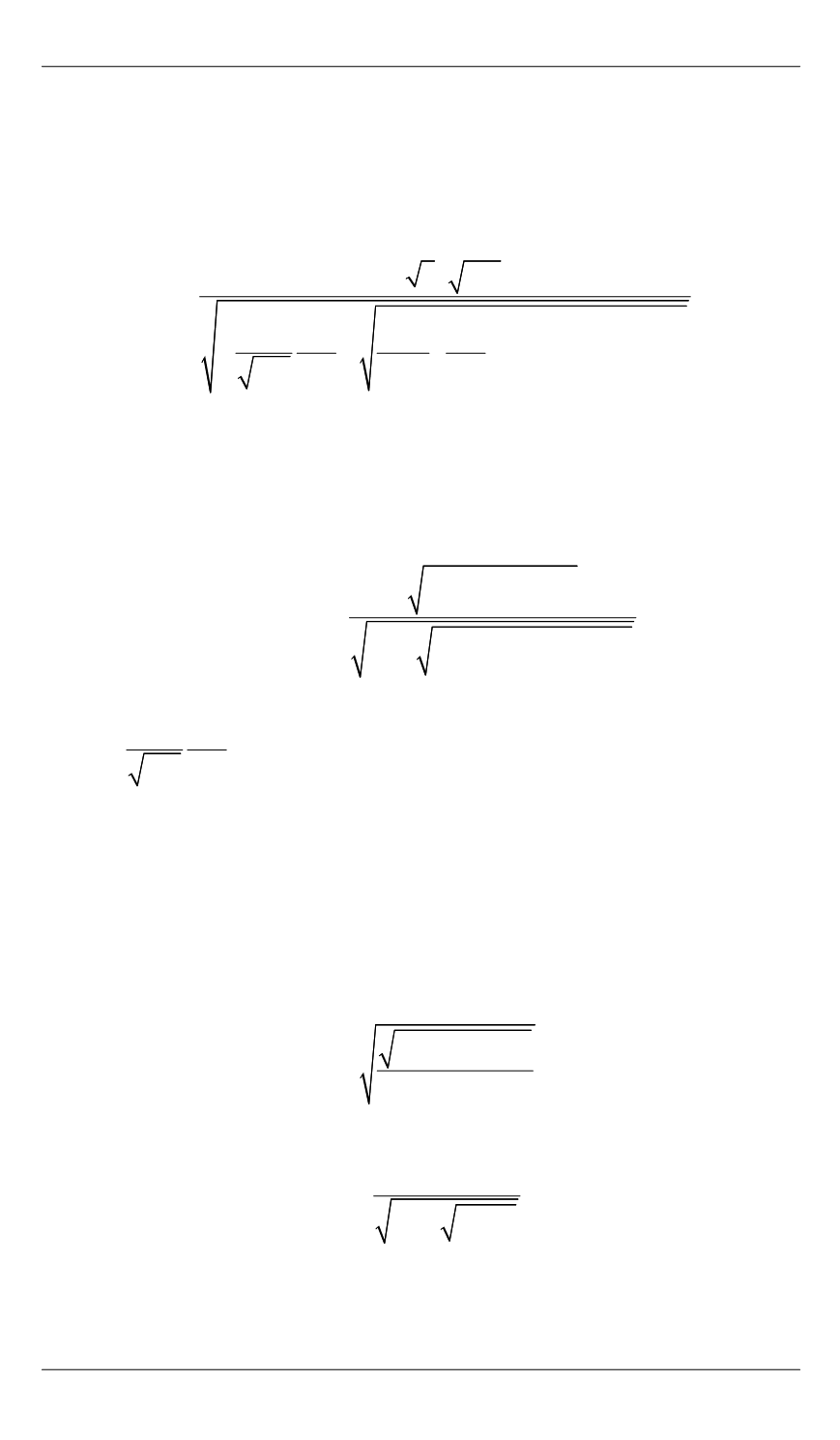
Таким образом
4
1,
1 1
(27)
где
– убывающая функция с вертикальной асимптотой в нуле, т. е.
в окрестности нуля стремится к бесконечности (рис. 2).


