Фазовые скорости бегущих волн в цилиндрической оболочке при конечной и бесконечной жесткости поперечного сдвига - page 5

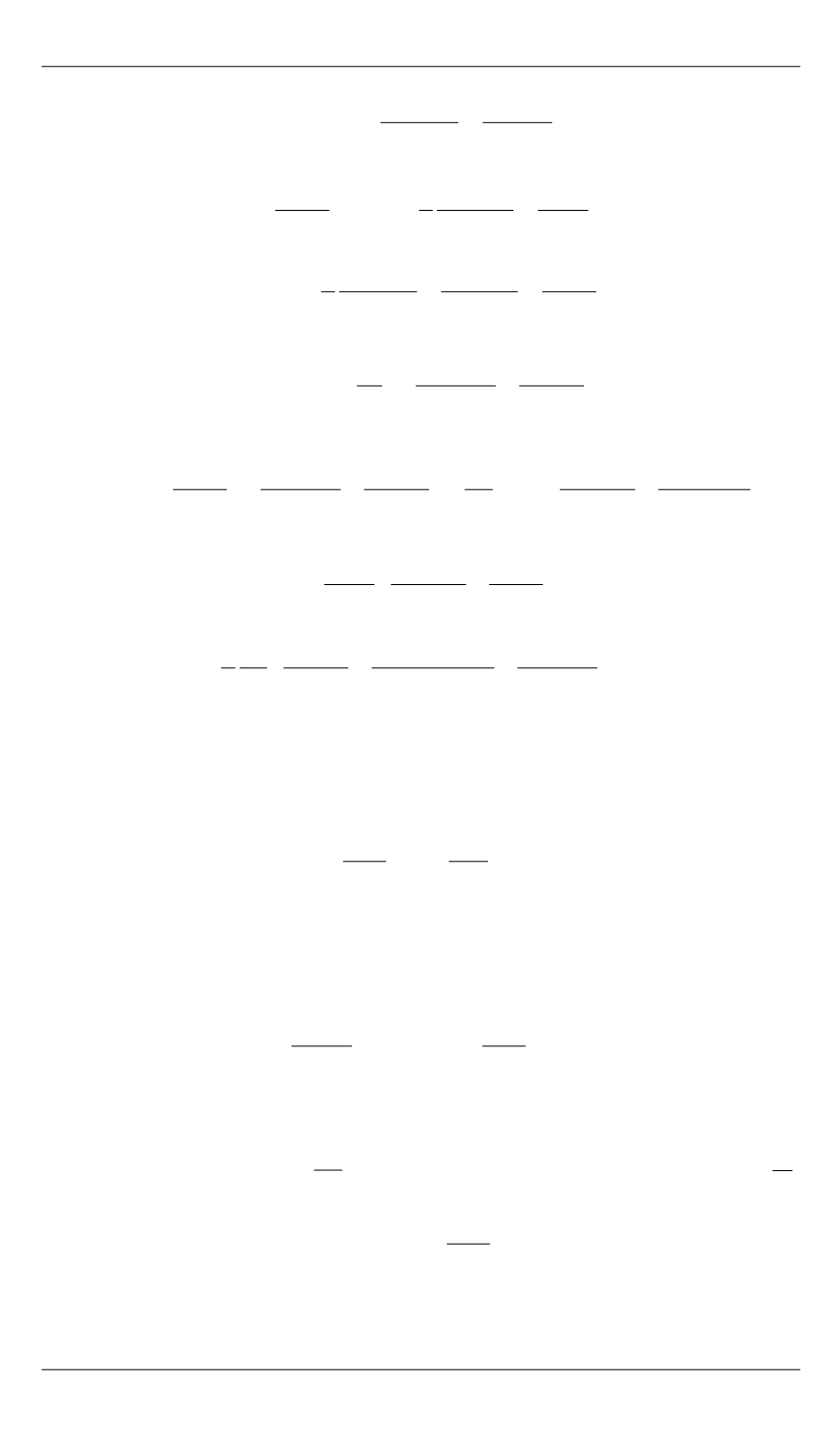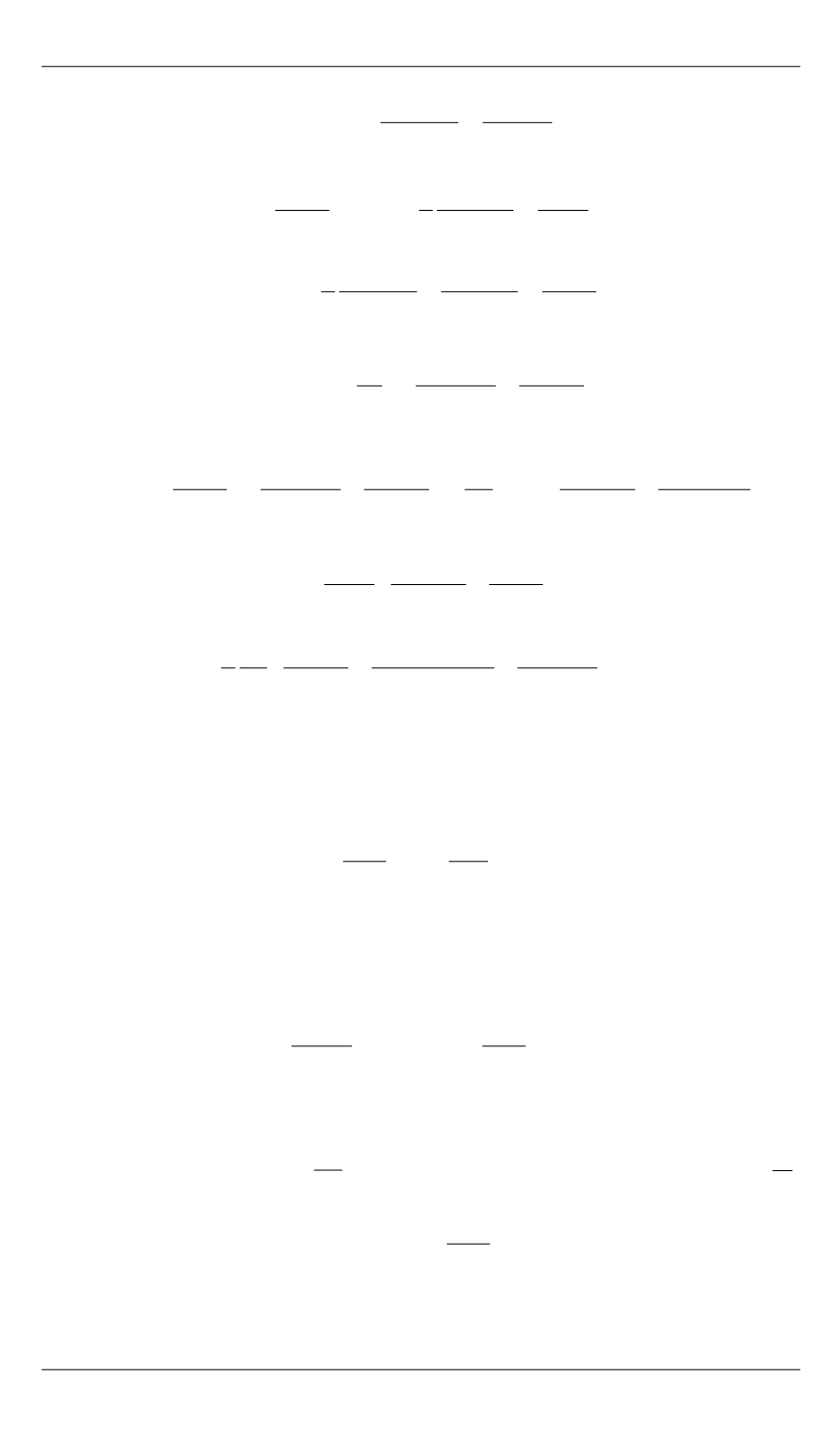
Фазовые скорости бегущих волн в цилиндрической оболочке при конечной и бесконечной …
5
( , ) ( , )
( , )
s
s
u s w s
s s R
  
   

,
cos 1 ( , ) sin
( , ) ( , ) ( , ) v s
s u s w s
r r r 
   
      

,
1 ( , ) ( , ) cos
( , ) ( , )
s
u s v s
s v s
r s r 
    
     
 
,
( , ) ( , )
( , )
s
w s u s
s s s R s
 
   
      
     
, (4)
2
2 2
cos ( , ) ( , ) 1 ( , ) ( , )
( , ) sin
s
w s u s v s w s
s r s R r 
           
             
  
   
,
sin ( , ) cos
2 ( , ) ( , )
1 ( , ) ( , ) cos ( , ) .
s
v s
s v s
r s r
u s w s w s
r R r s
s

     
     
 
  
 
     
    
   
 
Тогда в системе уравнений движения (2) первое уравнение при-
мет вид
2
2 0, s N u
r r h
s t
 
  
 
(5)
второе и пятое уравнения выполняются тождественно; остальные
преобразуем, выразив из четвертого s Q и подставив в третье:
2 2
2 2 0. s M w
r N r h
s t 
 
   
 
(6)
Подставим в полученные уравнения выражения для продольной
погонной силы 11 s
u
N С
s


 , поперечной погонной силы 22
w N C
r  
и продольного момента
2
11 2 s
w
M D
s
  
  
   

с учетом принятых допу-
щений и кинематической гипотезы. Получим систему уравнений
движения в перемещениях в случае гипотезы Кирхгофа – Лява: