О новом подходе в методе функций Грина при решении краевых задач Дирихле и Неймана для уравнения Лапласа - page 10

Э.М. Карташов
10
В математической физике эта задача считается классической и
стандартной, хотя ее решение связано с длительными вычислениями.
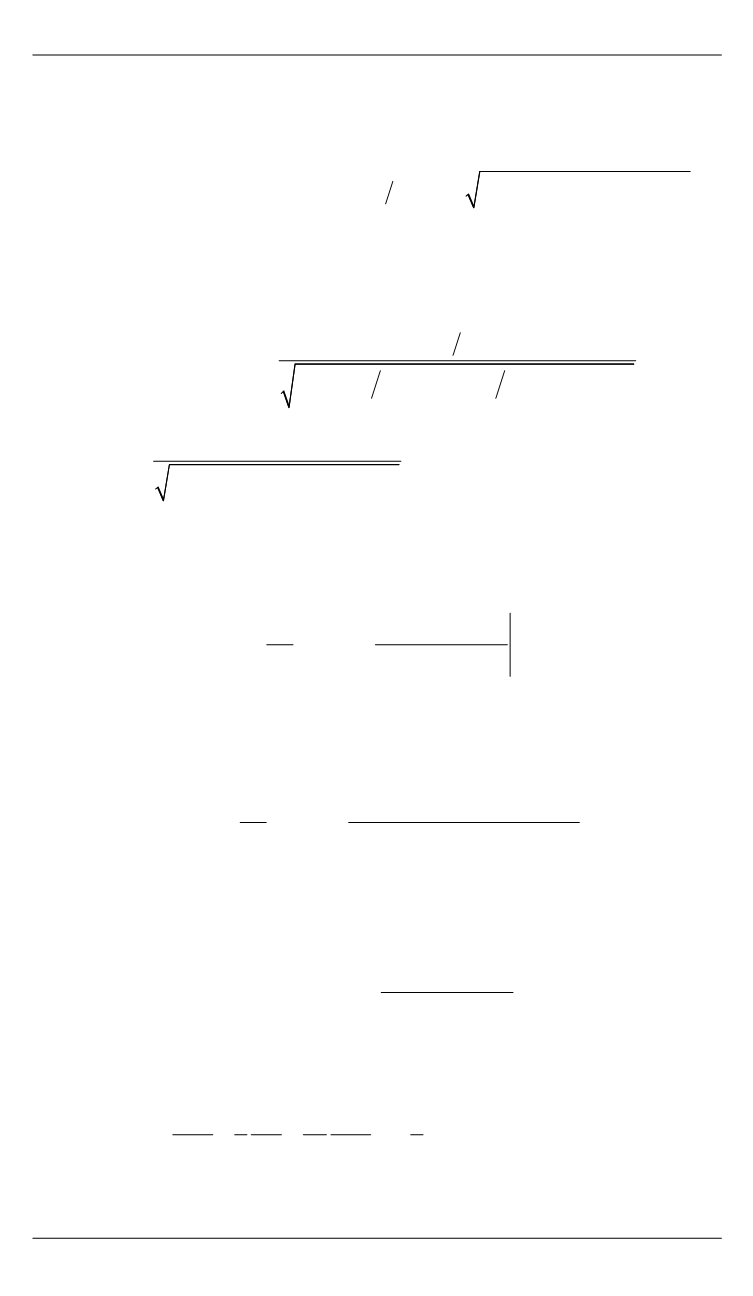
Согласно теории функции Грина    
, , , , , , G r r W r r          
 
, , , q r r      , где    
, , , ln 1 q r r      ,   2 2 2 cos , r r rr        а
 
, , , W r r    является решением задачи (6), (7), записанной для кру-
га в полярной системе координат, находим с использованием сопря-
женности точек относительно окружности [4]:
   
     
 
2 4 2 2
2 2
, , , ln
2 cos
1
ln .
2 cos
R r
G r r
r R r r R r
r r rr

     
       

       
(38)
Интегральное выражение (4), записанное для области, указанной
в (35), имеет вид
      2
0
, , ,
,
2 r R
G r r R
T r d
r


    
      
   
и с учетом (38) дает решение задачи (35) – (37) в виде интеграла
Пуассона для круга
     
2 2 2
2 2
0
1 ,
2 2 cos
R r
T r d
R r Rr
 
      
        . (39)
Решение задачи (35) – (37) можно записать и в виде интегрально-
го соотношения (12)
      2
0
, , ,
,
r R
G r r
T r R d
r


      
       
 

   , (40)
если исходить из определения функции Грина (8), (9), то
   
2 2
2 2 2
1 1 1 ,
0 , 0 2 ;
G G G r r
r r r r r
r R
              
  
     
(41)