
Е.А. Сухов, Б.С. Бардин
8
Инженерный журнал: наука и инновации
# 11·2017
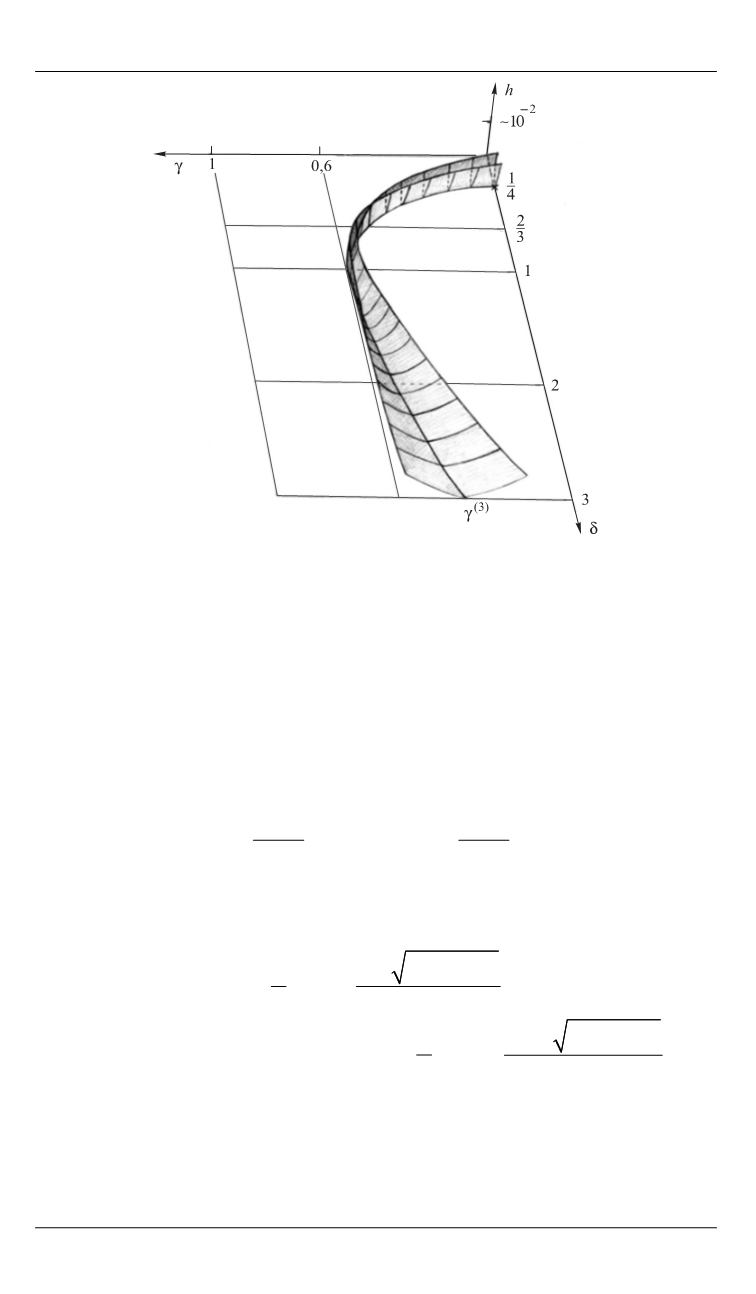
Рис. 3.
Граница области параметрического резонанса
в пространстве параметров
h
,
,
, полученная аналити-
чески при малых значениях параметра энергии
h
и всех
допустимых значениях кинематического
и инерцион-
ного
параметров
описывающую долгопериодические движения в окрестности границы
области параметрического резонанса.
Положения равновесия
*
2
Q
,
*
2
P
системы с гамильтонианом (13)
определяются уравнениями
IV
2
*
2
0;
∗
=
=
dK Q
dP
IV
*
2
*
2
0.
= − =
dK P
dQ
В зависимости от значений параметра
μ
число положений равнове-
сия будет различным. В области
1
Γ
(рис. 4,
б
) существует только поло-
жение равновесия
*
2
2
π=
Q
,
2
2
*
2
6
6
μ + μ + ε
=
ε
C
P
(I), в области
2
Γ
―
только положение равновесия
*
2
2
π = −
Q
,
2
2
*
2
6
6
−μ + μ + ε
=
ε
C
P
(II).
В области
3
Γ
существует как положение равновесия I, так и положе-
ние равновесия II. При малых значениях
μ
границы областей совпада-
ют с границей области параметрического резонанса и определяются
уравнением (11)
.
В переменных
, ,
,
ψ θ
ψ θ
p p
указанным положениям
















