
Численно-аналитическое построение и исследование устойчивости…
Инженерный журнал: наука и инновации
# 11·2017 9
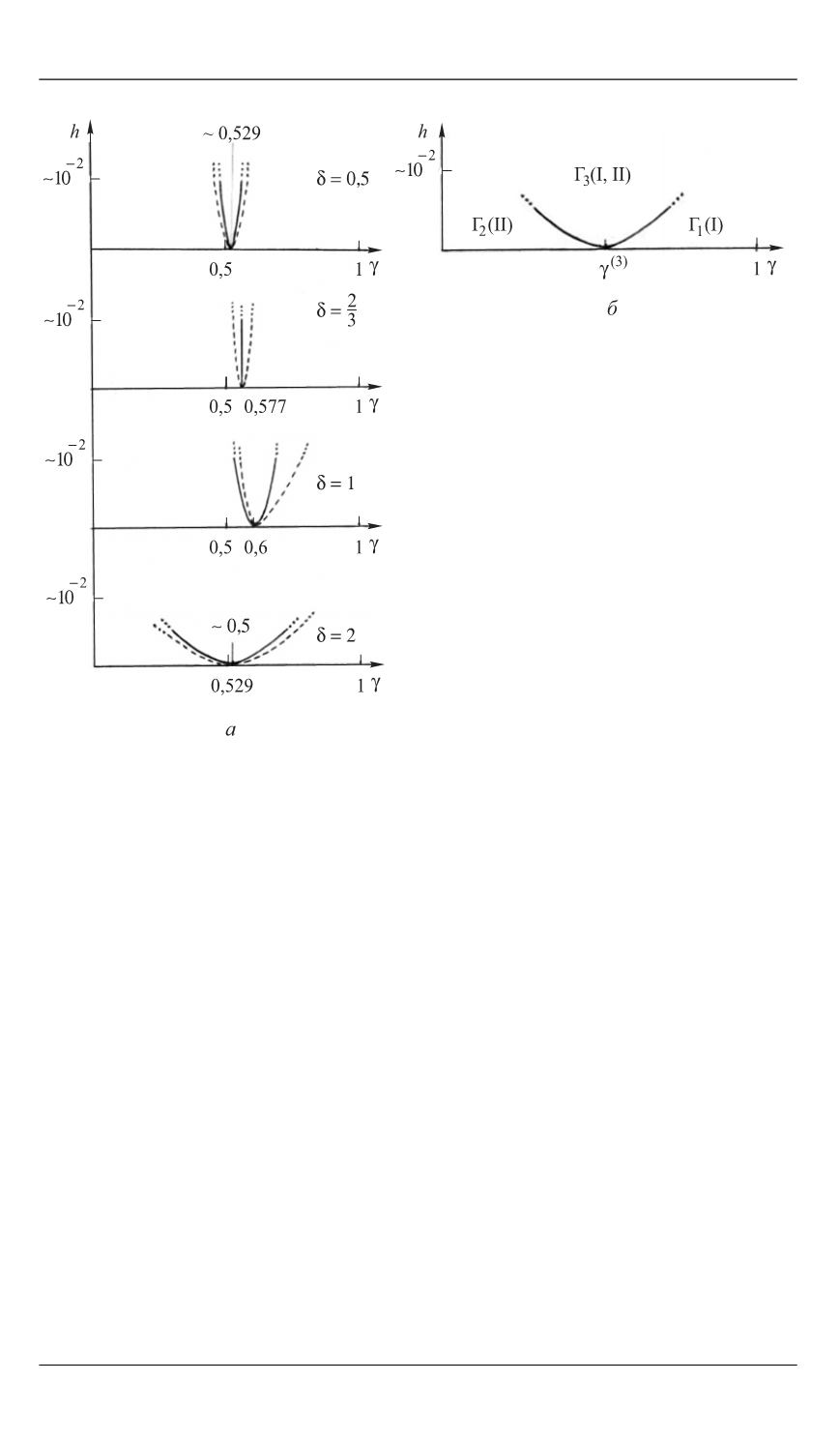
Рис. 4.
Взаимное расположение результатов численного (
пунктирные линии
) и
аналитического (
сплошные линии
) построения границы области параметрического
резонанса в плоскости
= const в случае
= 0,5;
= 2/3,
= 1 и
= 2 при малых
значениях параметра энергии
h
(
а
) и расположение семейств долгопериодических
движений относительно поверхности параметрического резонанса в сечении
= const
при малых значениях параметра
h
(
б
); в областях Г
1
и Г
2
существует по одному
семейству долгопериодических движений, в области Г
3
имеются два семейства
долгопериодических движений
равновесия соответствуют два семейства долгопериодических дви-
жений (которые далее также будем обозначать I и II).
В окрестности резонанса
2
1
2
ω = ω
семейства долгопериодических
движений I и II орбитально устойчивы в первом приближении [9].
С помощью численного метода, описанного выше, указанные семей-
ства были продолжены по параметрам до границ их существования
при значениях константы энергии
0,1.
≤
h
Результаты численного
исследования представлены на рис. 5–7, где через
(3)
γ
обозначена
кривая резонанса
2
1
2
ω = ω
, через
(4)
γ
― кривая резонанса
2
1
3
ω = ω
.
















