
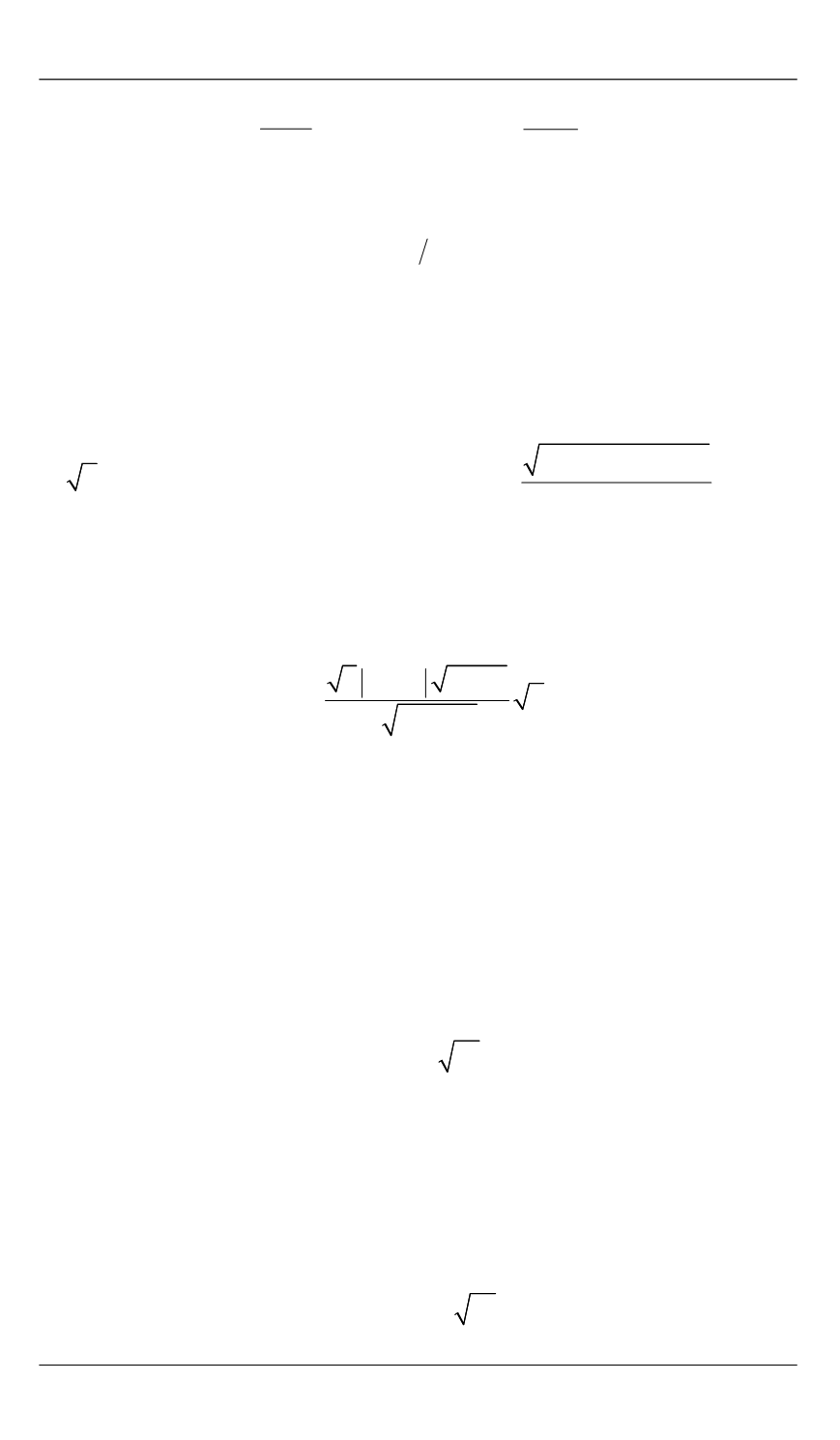
Численно-аналитическое построение и исследование устойчивости…
Инженерный журнал: наука и инновации
# 11·2017 7
*
2
2
( );
2 μ
= + ε
+
h C
O
2
*
2
1
8 .
= =
ε ω
A h
h nh
(9)
Второе равенство в (9) получено подстановкой (7) в (6). Подста-
вив в (8) выражение для параметра
C
из (9) и заменив коэффициент
невязки частот по формуле
2 1
2
μ = ω ω −
, получим следующее урав-
нение для границы области параметрического резонанса:
(
)
2
2
2
2 2
1
1
2
32
( ).
ω ω − ω = ω +
A h O h
(10)
Уравнение границы области параметрического резонанса в ис-
ходных параметрах станем искать в виде ряда
(3)
( , )
( )
γ δ = γ δ +
h
1
( ) ( )
+ γ δ +
h
O h
, где выражение
3
2
(3)
4 17 4
(
5
)
− δ + δ − δ
γ δ = ±
δ
задает
зависимость
γ
от
δ
при точном резонансе
2
1
2
ω = ω
. Подставив этот
ряд в (10) и приравняв коэффициенты при равных степенях
h
, опре-
делим
1
( )
γ δ
и получим уравнение границы области параметрическо-
го резонанса в пространстве параметров
, , :
γ δ
h
4
(3)
6 3 2 5 5
( , )
( )
25 (4
( )
)
δ − + δ
γ δ = γ δ ±
+
δ − δ
h
h O h
. (11)
Поверхность, задаваемая уравнением (11), показана на рис. 3.
При значениях
,
γ δ
, близких к резонансным, и малом
h
эта поверх-
ность хорошо аппроксимирует границы области параметрического
резонанса, что подтверждается совпадением результатов аналитиче-
ского и численного решения (см. рис. 3 и 4,
а
).
Для нахождения семейств долгопериодических движений вос-
пользуемся методикой, изложенной в работе А.П. Маркеева [9]. По-
средством замены переменных
1 2 1 2
1 2 1 2
, , ,
,
, ,
→
x x y y Q Q P P
гамильто-
ниан (6) можно привести к виду
(
)
III
2
1
2
1
2 2
2
2
sin( ) ( ),
= + μ + ε −
+ ε
K P P P P P Q O
(12)
где
1
2
2
≥
P P
.
Система с гамильтонианом (12) имеет первый интеграл
1
,
=
P C
где
C
― параметр, связанный с исходными параметрами задачи че-
рез соотношения (9). Используя первый интеграл и отбрасывая в (12)
члены выше первой степени по
ε
, получаем приближенную систему
с гамильтонианом
IV
2
2 2
2
( 2 )
sin( ),
= μ + ε −
K P C P P Q
(13)
















