
А.А. Стадухин, Р.Д. Песков
4
Инженерный журнал: наука и инновации
# 9·2017
его можно применять для вычис-
ления этих параметров, напри-
мер, как в программном продукте
Bullet Physic Engine [9], где для
каждого из контактирующих тел
создается по два многогранника
(внешний и внутренний): по внеш-
ним определяют факт пересечения
тел, по расстоянию между внут-
ренними — глубину проникно-
вения. Недостаток метода пред-
ставления контактирующего тела
в виде пары многоугольников —
низкая точность вычисления взаи-
модействия, особенно для тел с
выраженными острыми углами. Однако если одно из контактирующих
тел представляет собой окружность (колесо), существует способ полу-
чить точный расчет взаимодействия этих тел с помощью алгоритма
Гилберта — Джонсона — Керти.
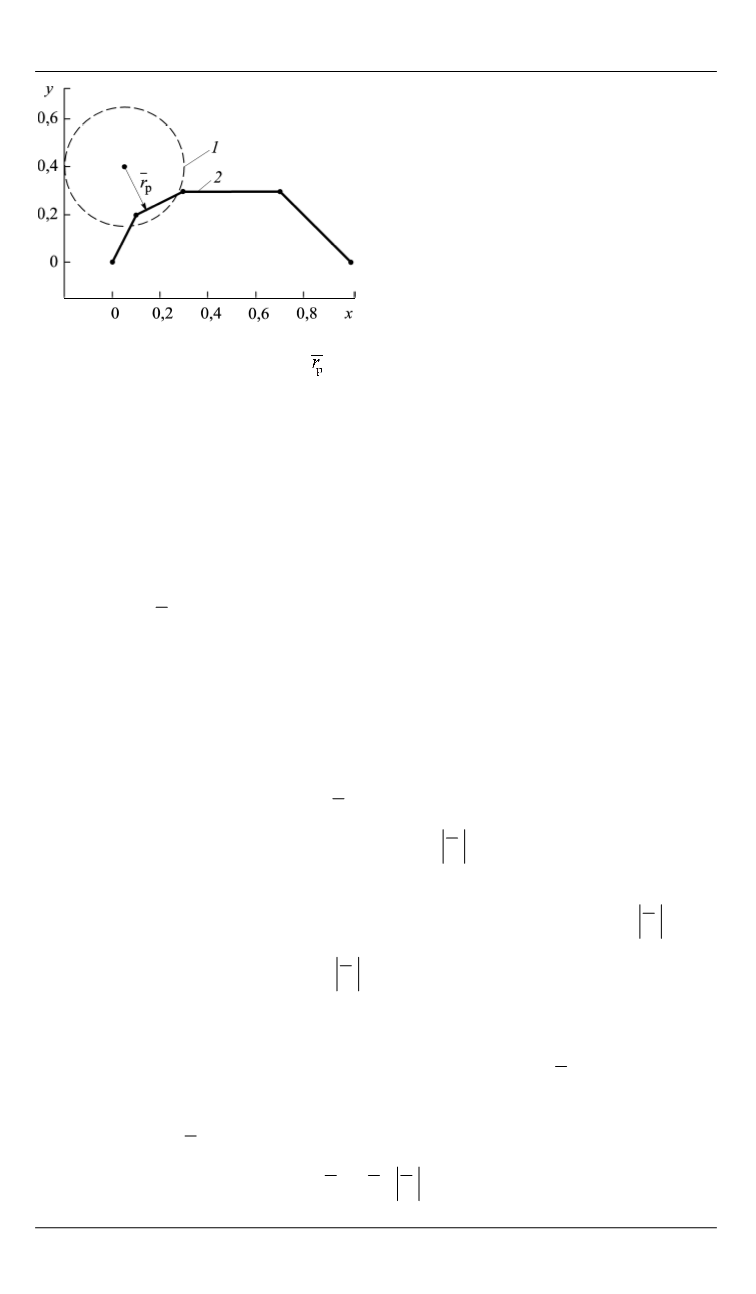
Итак, сведем рассматриваемую задачу к определению вектора
расстояния
р
r
от центра колеса до выпуклого многоугольника, пред-
ставляющего участок трассы (рис. 2). При такой постановке задачи
программная реализация алгоритма Гилберта — Джонсона — Керти
очень проста и обладает высокой производительностью.
На рис. 3 показаны промежуточные результаты работы алгоритма,
осуществляющего поиск кратчайшего расстояния от многоугольника
трассы до точки центра колеса, для случая, представленного на рис. 2.
После получения вектора
р
r
следует сравнить его длину с радиу-
сом
к
r
колеса (рис. 4). В случае если
к р
,
r r
имеет место взаимодей-
ствие колеса с ОП и можно определить величину прогиба колеса
к
и его радиус качения
кач
,
r
равный модулю вектора расстояния
р
:
r
к к р
,
r r
кач к к
.
r
r
Как видно из рис. 4, в случае взаимодействия колеса с выпуклым
многоугольником трассы возможно существование только одной
точки контакта
,
K
которая принадлежит вектору
р
r
и отстоит от
центра колеса
C
на расстояние
кач
.
r
Определим вектор, являющийся
ортом вектора
р
:
r
р р р
/ .
n r r
Рис. 2.
Определение вектора
от центра колеса до трассы:
1
— модель колеса;
2
— многоугольник
трассы
















