
А.А. Стадухин, Р.Д. Песков
12
Инженерный журнал: наука и инновации
# 9·2017
Решение пространственной задачи.
Как было сказано выше, все
результаты, представленные в статье, могут быть использованы при
решении пространственной задачи. С помощью алгоритма Гилберта —
Джонсона — Керти можно находить вектор расстояния
р
r
между точ-
кой центра колеса и пространственным многогранником трассы. Вели-
чину прогиба колеса в этом случае можно вычислить, если считать, что
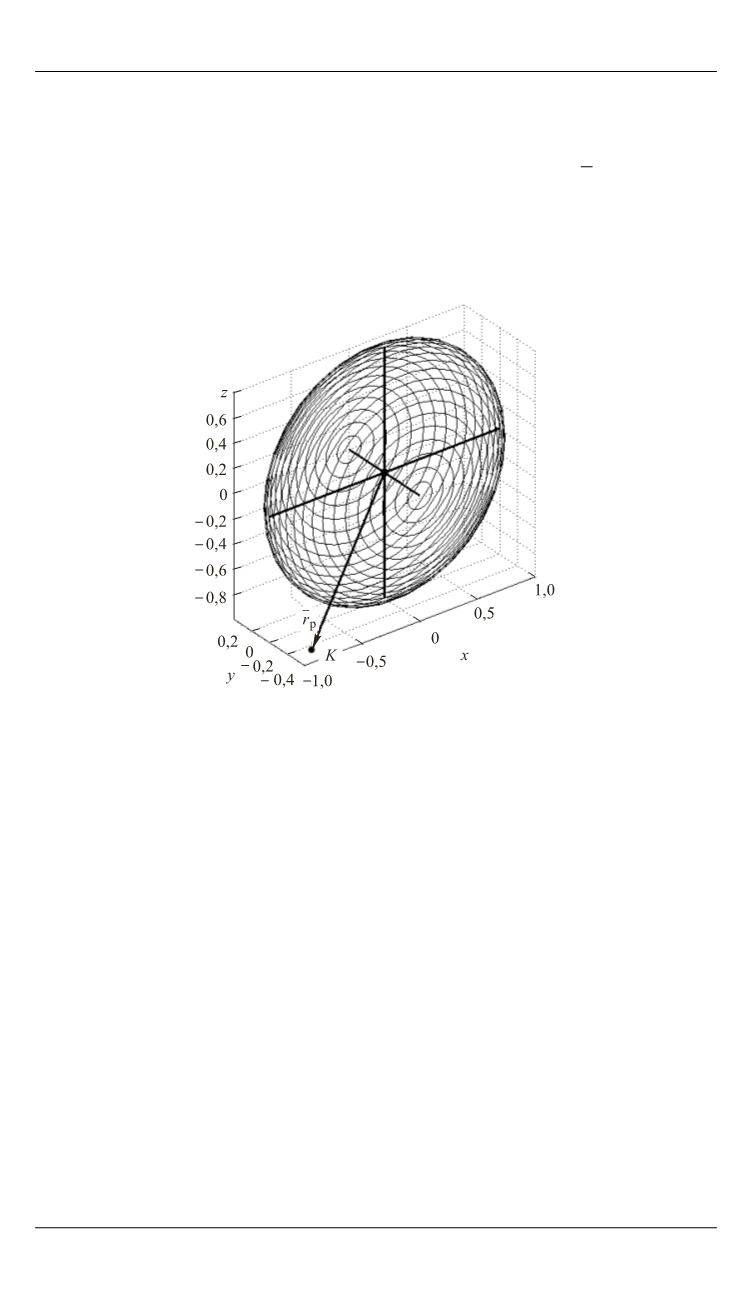
колесо имеет форму эллипсоида (рис. 12).
Рис. 12.
Представление колеса в виде эллипсоида
для пространственной задачи
В этом случае нормальные реакции всегда направлены к его цен-
тру. Прочие силы и моменты взаимодействия находятся аналогично
плоскому случаю, приведенному в данной статье.
Заключение.
Рассмотренные примеры моделирования с приме-
нением предлагаемого метода расчета сил взаимодействия колеса
и ОП показали качественное соответствие ожидаемому поведению
КМ на крупных препятствиях. Модель также позволила продемонст-
рировать известные ограничения профильной проходимости КМ.
Рассматриваемый метод может быть особенно полезен при ис-
следовании проходимости колесных мобильных роботов с изменяе-
мой геометрией ходовой части.
ЛИТЕРАТУРА
Мамити Г.И., Плиев С.Х., Васильев В.Г. Динамическое преодоление невы-
сокого порога полноприводным автомобилем.
Известия Горского государ-
ственного аграрного университета
, 2015, № 3, с. 152–157.
















