
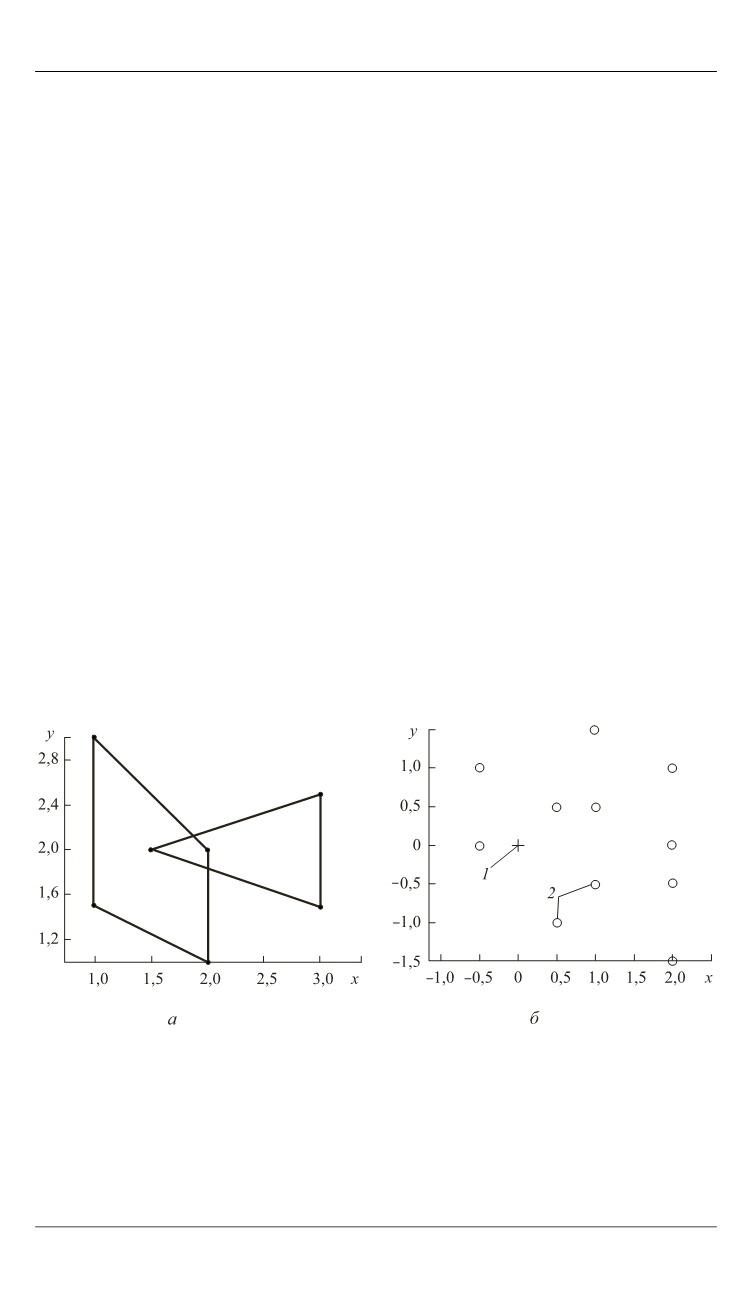
Исследование профильной проходимости колесной машины…
Инженерный журнал: наука и инновации
# 9·2017 3
описан в статье [6]. Алгоритм Гилберта — Джонсона — Керти был
разработан для эффективного определения расстояния между выпук-
лыми многогранниками и их пересечения в трехмерном простран-
стве. С незначительными изменениями алгоритм способен работать
и с пересечением многоугольников на плоскости. В настоящей статье
описания и рисунки ограничены плоским случаем, однако все ре-
зультаты могут быть распространены на пространственные модели.
Алгоритм Гилберта — Джонсона — Керти берет за основу тот
факт, что геометрическая фигура CSO (согласно терминологии авто-
ров алгоритма), составленная из разности координат каждой вершины
одного пересекающегося многогранника и каждой вершины другого
(разность Минковского), содержит начало координат пространства,
полученного вычитанием (рис. 1). Если многогранники не пересека-
ются, то вектор расстояния от крайней точки, грани или плоскости фи-
гуры CSO до начала координат является вектором расстояния между
многогранниками. При этом необязательно вычислять фигуру CSO
целиком (она состоит из большого числа точек), достаточно находить
самые дальние в заданном направлении точки CSO по одной. В каче-
стве направления поиска необходимо использовать вектор, направлен-
ный от симплекса (простейшей фигуры, составленной из найденных
ранее точек) к началу координат. Критерием остановки поиска обычно
считают невозможность найти точку фигуры CSO, образующую сим-
плекс, который находится ближе к началу координат, чем симплекс,
состоящий из найденных ранее точек.
Рис. 1.
Пересекающиеся многоугольники (
а
) и их фигура CSO (
б
):
1
— начало координат;
2
— вершины фигуры CSO
Важно отметить, что использование алгоритма Гилберта — Джон-
сона — Керти не позволяет определить расположение точек контакта,
глубину и направление проникновения пересекающихся тел. Однако
















