
Нгуен Зуй Хунг, А.Н. Темнов
8
Инженерный журнал: наука и инновации
# 5·2016
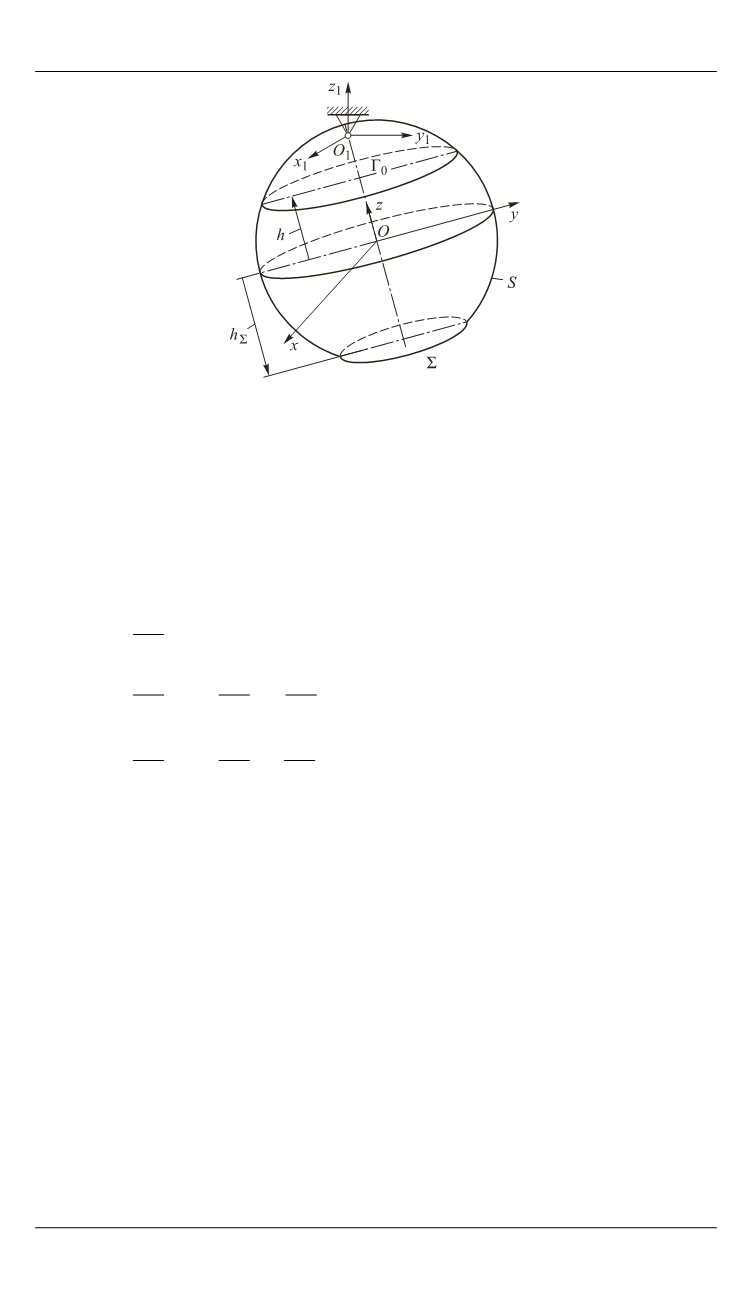
Рис. 5.
Основные параметры и системы координат
для задачи о колебаниях бака сферической формы,
частично заполненного жидким топливом
Формулировка краевой задачи в цилиндрической и сферической си-
стемах координат (
r
,
,
z
) и (
R
,
,
) записана в безразмерной форме [8]:
0Г
0
0
0
0
(0)
0 в ;
sin sin на ( = 1);
0 на Г (
);
(
)
0 на (
);
( , , , )
при = 0,
ez
ez
L
S R
R
V
dt V V
z h
t
z
z
V
V V
z h
t
z
z
r z t
t
(12)
где
— малый угол поворота бака вокруг оси
1 1
;
O x
L
—
расстоя-
ние между центрами
О
и
О
1
систем координат;
V
ez
— проекция на
ось
O
z
вектора скорости переноса жидкости.
Для того чтобы легче отыскать потенциал скоростей
, предста-
вим его в виде суммы трех функций [9]:
1
2
( , , , )
( , , ) ( )
( , , ) ( )
( , , ) ( ).
r z t
r z t
r z s t
r z p t
(13)
Выберем выражение для функций
F
и
1 1
,
s
2
2
p
таким образом, чтобы первое граничное условие системы (12) удо-
влетворялось с помощью функции
,
F
а второе и третье граничные
условия — с помощью суммы функций
F
и
1 2
,
.
Используя вариационный метод, получим выражения для функ-
ций
1 2
, ,
[5]
:
















