
Задачи динамики космических конструкций с жидким топливом…
Инженерный журнал: наука и инновации
# 5·2016 7
0 ( 0);
m
x
0 ( 1).
m
m
d
r
x
dx
Уравнения (9), (10) можно записать в виде следующей системы:
1
;
2
,
1, 2, ...,
m m m m m m
m m m m
K N C
Q
a
m
(11)
где
m
K
,
m
N
,
m
Q
— соответствующие интегральные операторы.
В табл. 2 приведено численное решение уравнения (8) и системы
уравнений (11), а на рис. 4 представлена форма неосесимметричных
колебаний (
m
= 1) первого и второго тона.
Таблица 2
Собственные числа первого и второго тона
Bo
z
0
0
, град
По методу Ритца
По интегральной форме
11
12
11
12
5
0,1
90
8,35916
177,56868
8,42555
189,46028
1
–0,1
75
1,50904
143,02293
1,54596
143,51107
8
–0,2
25
13,95616
144,54376
18,05670
167,27630
10 –0,2
20
16,57549
143,32583
20,97530
174,36390
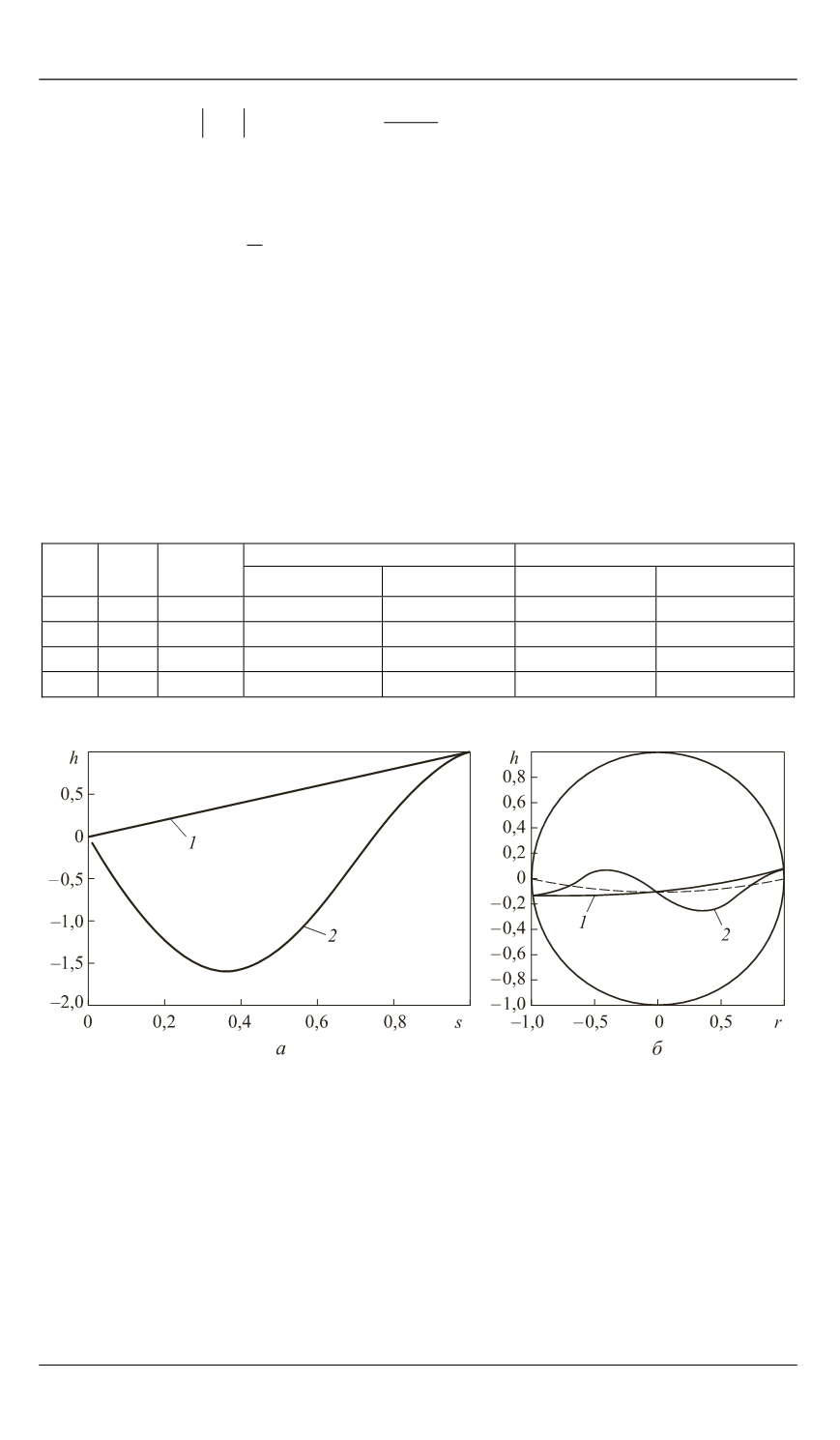
Рис. 4.
Формы колебаний первого (
1
) и второго (
2
) тона при Bo = 1,
z
0
= –0,1 и
0
= 80
:
а
— от криволинейной координаты
s
;
б
— в сферической полости
Колебания бака сферической формы, частично заполненного
жидким топливом.
Рассмотрим задачу о колебаниях вращающегося
вокруг оси
1 1
O x
бака сферической формы с полостью, которая ча-
стично заполнена жидкостью, вытекающей через заборные устрой-
ства из бака (рис. 5).
















