
Задачи динамики космических конструкций с жидким топливом…
Инженерный журнал: наука и инновации
# 5·2016 5
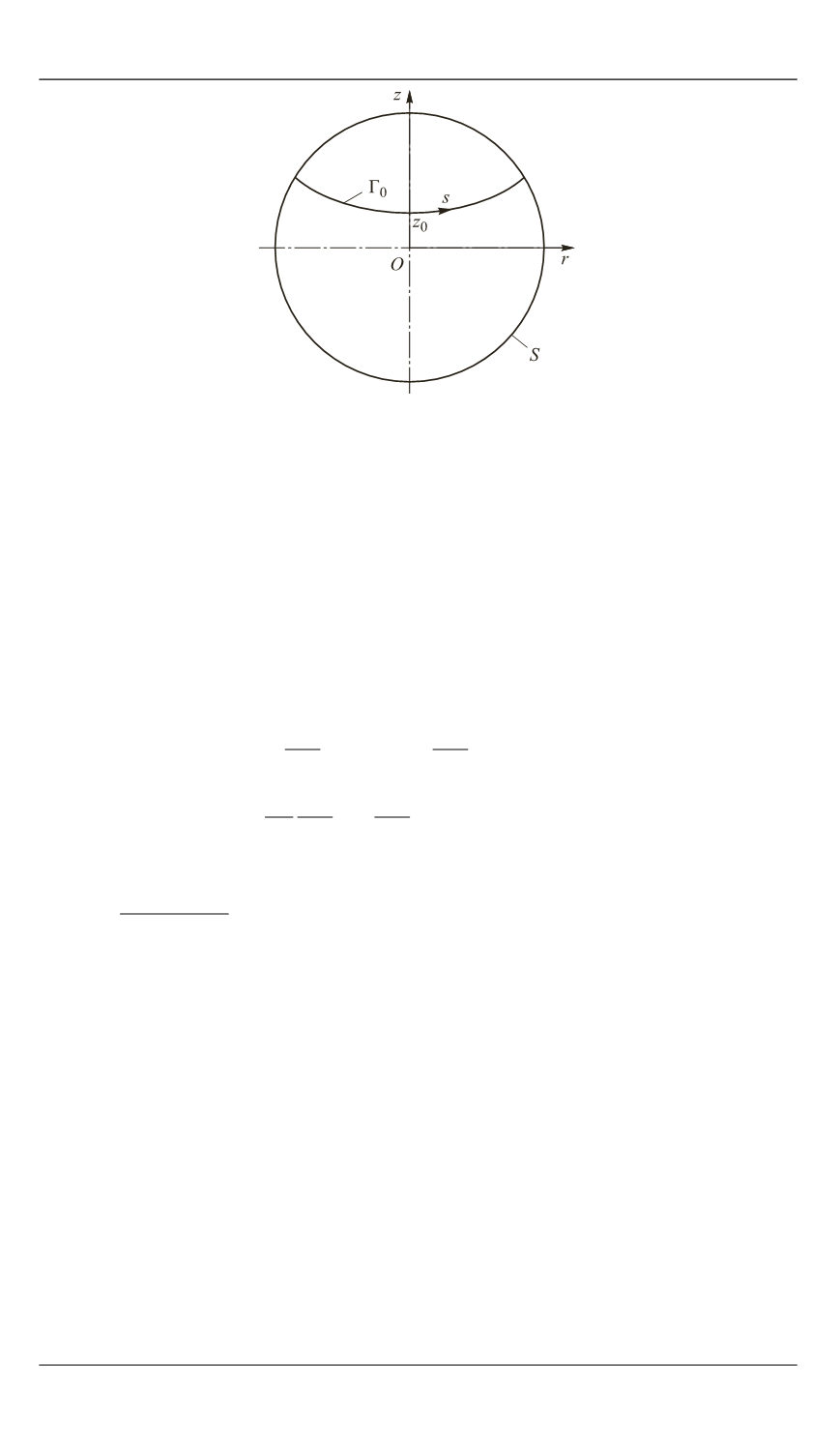
Рис. 3.
Основные параметры и система
координат для задачи о колебаниях жид-
кости в условиях, близких к невесомости
Постановка задачи
. Как известно [6], задача о малых колебаниях
жидкости в сферическом баке с учетом сил поверхностного натяжения
описывается в безразмерной форме следующей системой уравнений:
Г
0 в ;
/
0 на ;
(
)
на Г;
0 на ,
n
S
B a
n
n
l
n
n
(6)
где
1
0
0
cos
;
sin
k
k
2 2
1 2
Bocos( , )
a
n z k k
2 1
(Bo
);
gR
2 3 1
.
R
Здесь
В
— положительно сопряженный оператор;
Г
— оператор
Лапласа — Бельтрами на поверхности Г;
0
— угол смачивания;
k
—
кривизна меридионального сечения бака;
1
k
и
2
k
— главные кривиз-
ны поверхности Г, причем
1
k
— кривизна линии
L
0
пересечения по-
верхности Г с плоскостью (
r
,
z
);
l
— линия пересечения поверхности Г
со стенкой бака;
— внешняя нормаль к контуру
l
в плоскости, ка-
сательной к поверхности Г;
— плотность жидкости; Bo — число
Бонда;
g
— интенсивность гравитационных сил;
— коэффициент
поверхностного натяжения.
Вариационная формулировка задачи и реализация метода Ритца.
Краевая задача (6) допускает эквивалентную вариационную форму-
лировку: определение стационарных точек функционала [6]
















