Модилирование динамической устойчивости цилиндрической оболочки…
3
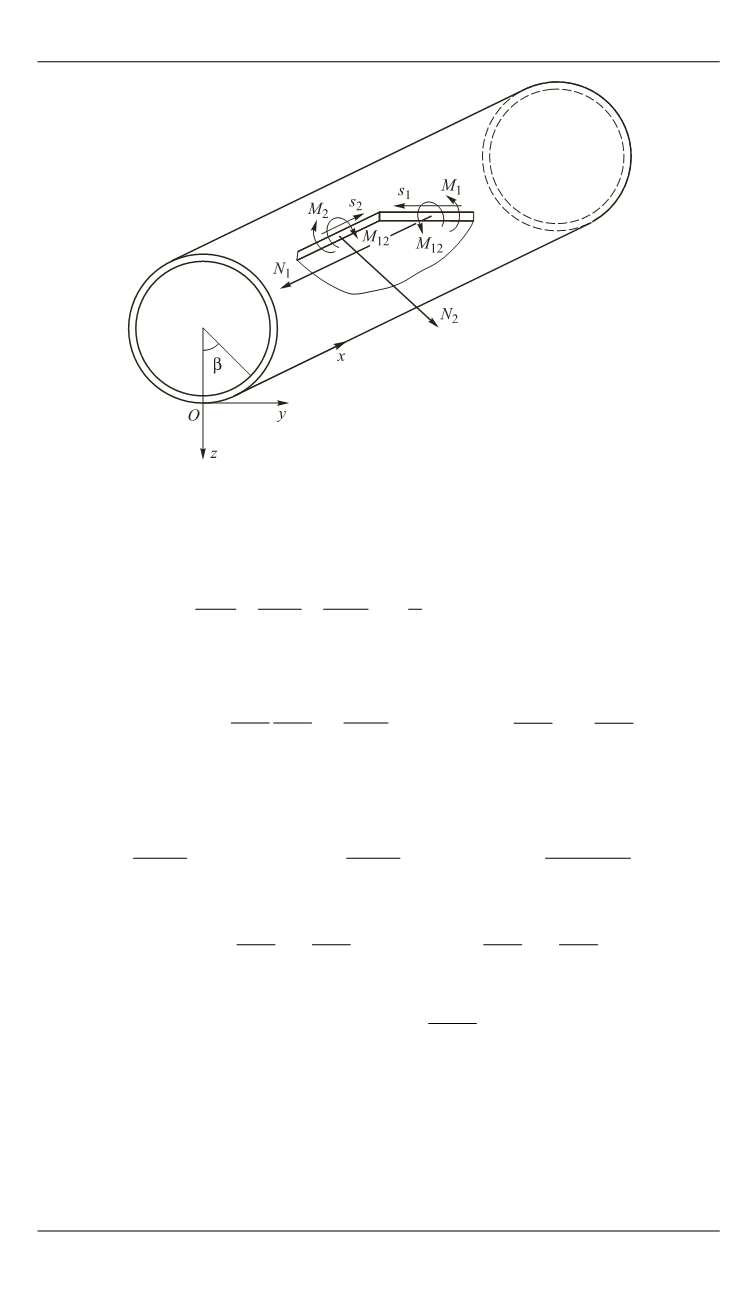
Рис. 2.
Схема внутренних сил и моментов в произвольном сечении
оболочки
Эти величины связаны уравнением совместности деформаций
2
2
2
2
1
2
2
2
1 ( , )
2
k
L w w w
x y
y
x
,
(1)
где
2
2 2
2
2 2
( , ) 2
;
w w w
L w w
x y
x y
2
2
2
2
1 2
2
k
w w
k
k
x
y
.
При этом соотношение Гука можно представить следующим об-
разом:
1
1
2
2
,
1
E
2
2
1
2
,
1
E
2
,
2 1
E
2
2
1
2
2
,
w w
M D
x
y
2
2
2
2
2
,
w w
M D
y
x
2
12
1
.
w
M D
x y
Здесь
1 2
, ,
— нормальные и касательные напряжения в срединной
поверхности оболочки;
E
,
— модуль упругости и коэффициент
Пуассона материала оболочки.
Уравнения равновесия произвольного элемента оболочки можно
записать в виде


