В.М. Дубровин, Т.А. Бутина
10
Если принять, что интенсивность давления возрастает в соответ-
ствии с законом
,
q st
и обозначить
2
2
в
,
stR t
E q
уравнение (14) можно
представить в виде
2 2 3
2
0
2 2
0
1
0
2
2
2
2
2
1
d s t
B
B
dt
N N
2
0
0 0
3
4
2
2
2
1
2
1
0,
B
B
N N N N
(15)
где
2
1 1 2
в
;
B c
q
2
3
2 2
в
;
4
N B c
q
3 3
3
в
;
2
c N B
q
2
2 3
4
в
1 1
2 ;
8
c c
B
q
2
4
2
3
в
1
;
2
CE
s
q
sR R
c
— скорость звука в материале обо-
лочки.
Решение уравнения (15) позволит определить критическое динами-
ческое внешнее давление, которое затем можно сравнить с критическим
давлением при статическом приложении нагрузки. Чтобы выполнить
сравнение, введем понятие коэффициента динамичности
д
K
критиче-
ской нагрузки, равного отношению динамической критической нагруз-
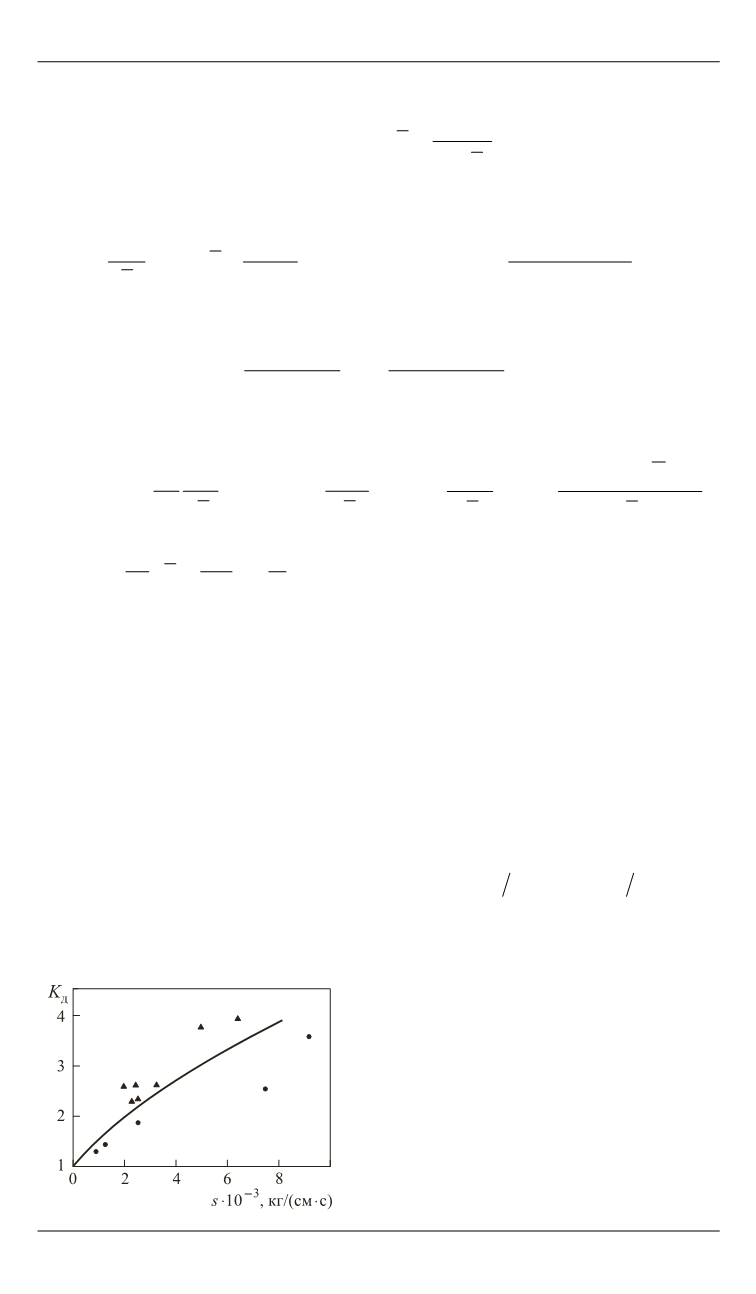
ки к верхнему статическому значению критической нагрузки. На рис. 3
представлен коэффициент
д
K
в зависимости от скорости нагружения,
полученный расчетом критической нагрузки по формуле (15). Расчеты
проводились для оболочки с параметрами:
0, 45;
R l
11, 2;
R
0
0,001;
5
7, 75 10
E
кг/см
2
;
5
5 10
с
см/c. Также приведены экс-
периментальные значения
д
K
по данным
[1] (см. рис. 3).
Рис. 3.
Зависимость коэффициента ди-
намичности критической нагрузки ци-
линдрической оболочки от скорости
нагружения под действием внешнего
давления (
▲
— экспериментальные
данные для оболочки без начального
погиба;
— экспериментальные дан-
ные для оболочки с начальным погибом)


