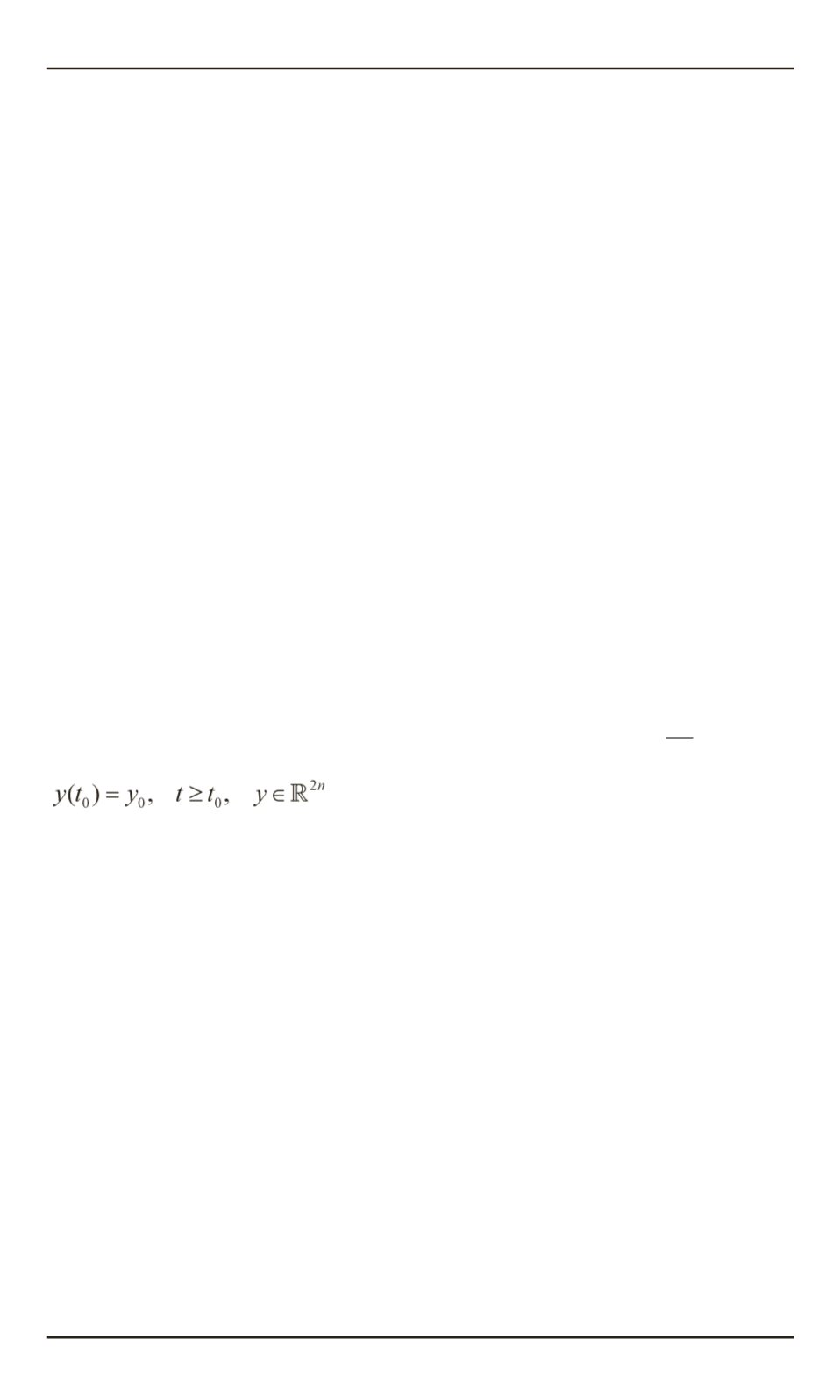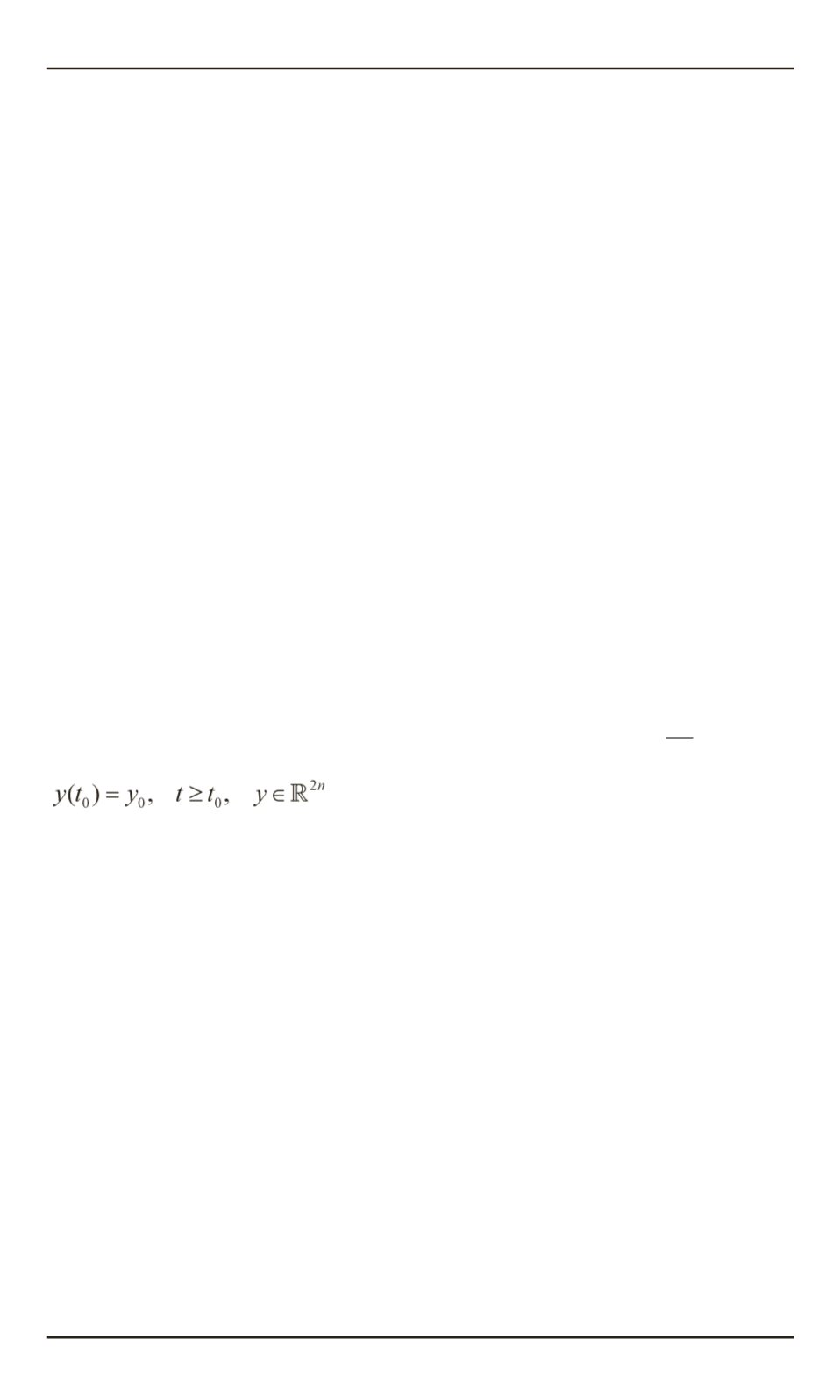
11
Математическое моделирование механических систем
ную земную плоскость совершает работу
( )
( )
(
)
1
1
1
1
1
1
1
sin
cos
,
y
z
R b
R b
ϕ −
ϕ δψ
а проекция момента
( )
1
M
G
на горизонтальную земную плоскость совер-
шает работу
(
)
(1)
(1)
1
1
1
cos
sin
.
y
z
M
M
ϕ −
ϕ δψ
В итоге
(
)
(
)
(1)
(1)
(1)
(1)
4
1
1
1
1
cos
sin .
y
z
y
z
Q M R b
R b M
= −
ϕ −
+
ϕ
Аналогично
получим
(1)
(1)
(1)
(1)
(1)
5
1
1
1
1
6
(
) cos (
)sin ,
,
z
y
y
z
x
Q M R b
M R b
Q M
= +
ϕ + −
ϕ =
(2)
(2)
(2)
(2)
7
2
2
2
2
(
) cos
(
)sin ,
y
z
y
z
Q M R b
R b M
= −
ϕ −
+
ϕ
(2)
(2)
(2)
(2)
(2)
8
2
2
2
2
9
(
) cos
(
)sin ,
.
z
y
y
z
x
Q M R b
M R b
Q M
= +
ϕ + −
ϕ =
Таким образом, получены аналитические выражения кинетическо-
го потенциала
L
=
T
– П и обобщенных сил
1 2
, ,...,
n
Q Q Q
как функций
обобщенных координат
1 2
, ,...,
n
q q q
обобщенных скоростей
1 2
, ,...,
n
q q q
и времени
t
. Аналитический этап математического моделирования ди-
намической системы СГП можно считать завершенным.
Решение начальной задачи Коши для гамильтоновой системы.
Наличие проблемы численного нахождения градиента кинетического
потенциала заставило привлечь многошаговый метод численного инте-
грирования. Численное решение начальной задачи Коши
( , ),
dy f y t
dt
=
строится в виде сеточной функции
{
}
0 1
1
, ,..., ,
,...,
n n
N
y y y y
y
+
на равномерной сетке
{
}
0 1
1
, ,..., ,
,...,
,
n n
N
t t
t t
t
+
где
0 1
1
...
...
n n
N f
t t
t t
t
t
+
< < < < < < ≤
с шагом
h
=
t
n
+1
–
t
n
. Дифференци-
альному уравнению на
n
-м шаге соответствует равносильное инте-
гральное
( ) ( )
( )
1
1
(
, ) .
n
n
t
n
n
t
y t
y t
f y t t dt
+
+
= +
∫
Заменив подынтегральную
вектор-функцию
( )
(
)
,
f y t t
полиномиальным интерполянтом
( )
,
k n
P t
степени
k
, построенным на (
k
+ 1) точечном фронтовом отрезке данных
(
) (
) (
)
{
}
1
1
,
,
,
,..., ,
,
n k n k
n k
n k
n n
t
f
t
f
t f
−
−
− + − +
где
(
)
,
n
n n
f
f y t
=
и
( )
,
n
n
y y t
≈
по-
лучим явную
k
-шаговую формулу Адамса:
( )
1
1
,
.
n
n
t
n
n
k n
t
y y
P t dt
+
+
= +
∫
При
k
= 5 это явная 5-шаговая экстраполяционная формула
Адамса—Башфорта