Простое построение совершенных стегосистем на основе различных ошибок…
7
S C S S
C C
x x P x P x
.
(8)
Из утверждения (8) легко видеть, что
2
2
log
log 1 0.
C C
S C
S S
P x
x x
P x
(9)
Подставляя результат формулы (9) в определение относительной
энтропии
(см. формулу (1)), получим, что
0.
C S
D P P
Следова-
тельно, стегосистема является
совершенной системой (от пассивного
противника)
. ►
Замечание. Условие леммы о декодировании помехоустойчивого
кода с почти достоверной вероятностью и условие, что
,
C
S
Y y Y y
вполне естественны. В дальнейшем будем считать, что эти условия
всегда выполняются и что любая
идеальная стегосистема
является
совершенной
. (Заметим, что обратное утверждение неверно — не лю-
бая совершенная стегосистема будет идеальной.) Таким образом,
«идеальность» является достаточным условием для «совершенности»
стеганографической системы.
Пример математической модели возникновения ошибок.
Рас-
смотрим математическую модель (ММ) возникновения ошибок,
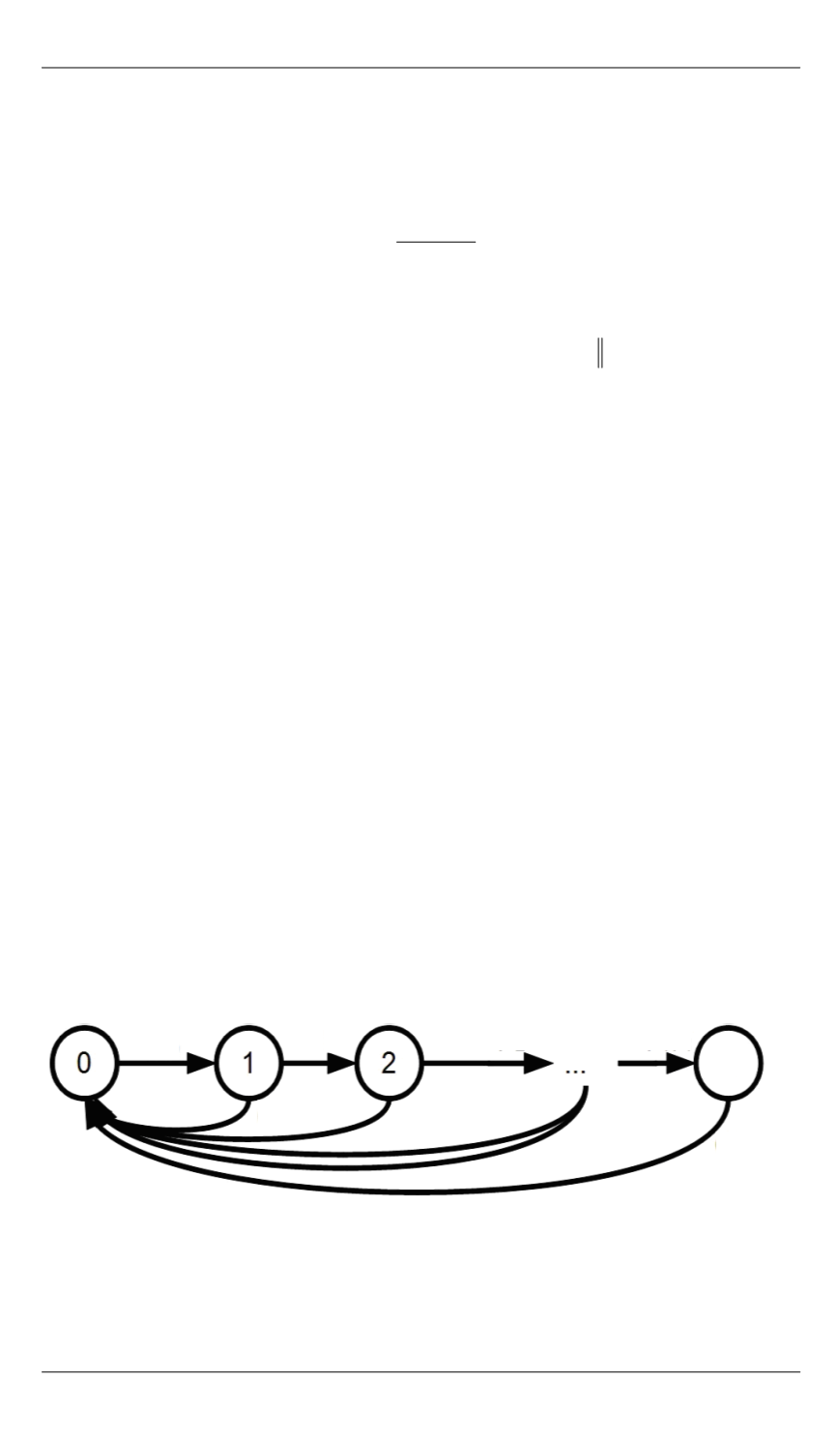
представленную на рис. 3. Эта модель разработана нами при проек-
тировании аппаратно-программного решения, реализующего стега-
нографию в кодах исправления ошибок на оптических дисках. Со-
бранных нами статистических данных пока недостаточно, чтобы го-
ворить об адекватности рассматриваемой ММ для оптических
дисков. Однако в рамках настоящей статьи воспользуемся этой моде-
лью в качестве примера реализации совершенной стеганографиче-
ской системы.
0
P
1
P
2
P
1
N
P
N
1
Q
2
Q
1
N
Q
Рис. 3.
Математическая модель возникновения ошибок на оптическом диске
При чтении уже записанного диска система находится в состоя-
нии 0. Ошибка произойдет с вероятностью
0
.
P
Если ошибка произо-


