П.В. Слипенчук
4
Если система совершенная, это означает, что, получая на вход кон-
тейнер, мы не можем с вероятностью, отличной от 0,5, определить,
принадлежит ли он к стегоконтейнеру или к пустому контейнеру.
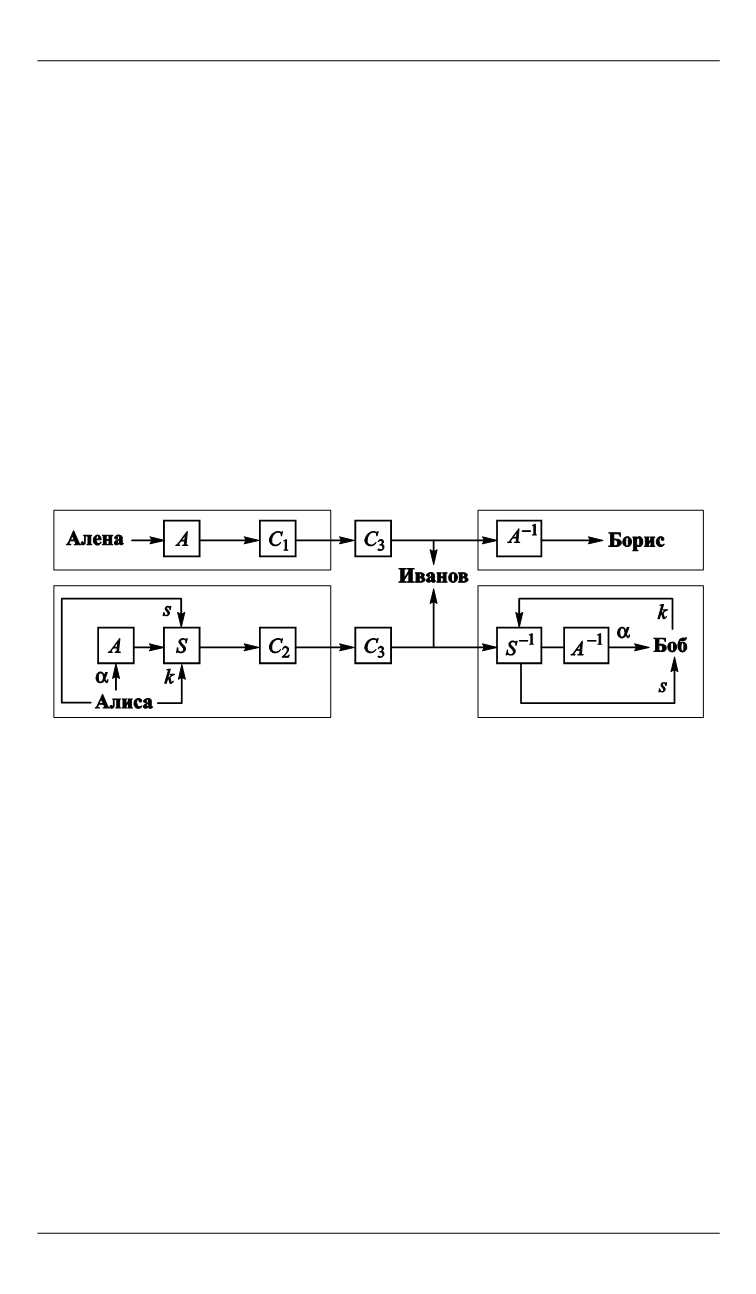
Модель трех каналов и идеальная стегосистема.
Описание мо-
дели трех каналов впервые приведено в работе [2]. В данной модели
выступают пять сторон: Алиса, Боб, Алена, Борис и Иванов. Одна из
задач Иванова определить, какая пара использует стеганографию при
передаче сообщения: Алиса и Боб или Алена и Борис.
Алена и Борис передают друг другу контейнеры, не содержащие
стегосообщения (пустые контейнеры) (рис. 2). Для этого Алена ис-
пользует
помехоустойчивый код
. Перед отправкой
информационный
вектор
подается на кодер
A
, который выдает на выходе
кодовый век-
тор
. После прохождения кодового вектора через каналы
1
C
и
3
C
Борис декодирует его и получает
информационный вектор
.
Рис. 2.
Модель трех каналов
Алиса перед отправкой кодового вектора вкрапляет в него сооб-
щение
s
. Таким образом,
кодовый вектор
(получаемый из информа-
ционного вектора α) выступает в качестве
контейнера
для
стегосо-
общения,
а сообщение представляет собой
искусственные ошибки
[2]. Позиции, содержащие стегосообщение, определяются неким ал-
горитмом
S
, зависящим от ключа
k
. Таким образом, Боб, зная ключ
k
и алгоритм
S
, может отличить искусственные ошибки от подлинных,
а Иванов не может.
Заметим, что модель трех каналов
есть частный случай модели Ка-
шена. Действительно, в модели трех каналов Алиса — это то же самое,
что Алиса в активном состоянии в модели Кашена, а Алена — это Али-
са в пассивном состоянии. Задача Иванова — определить, кто передает
скрытые сообщения — Алиса или Алена (см. рис. 2); задача Евы —
определить, когда Алиса активна (см. рис. 1). Пусть на вход канала
i
C
подается последовательность битов длиной
n
(см. рис. 2). Каждую
ошибку можно представить
n
-ричным числом в двоичной системе
счисления. Для каждой последовательности битов введем вероят-


