С.Б. Одиноков, Г.Р. Сагателян, А.Б. Соломашенко, Е.А. Дроздова
6
где
ε
— коэффициент асимметрии прямоугольной фазовой решетки,
рассчитываемый по формуле
1
2
a
d
ε = −
;
n
— показатель преломления стекла.
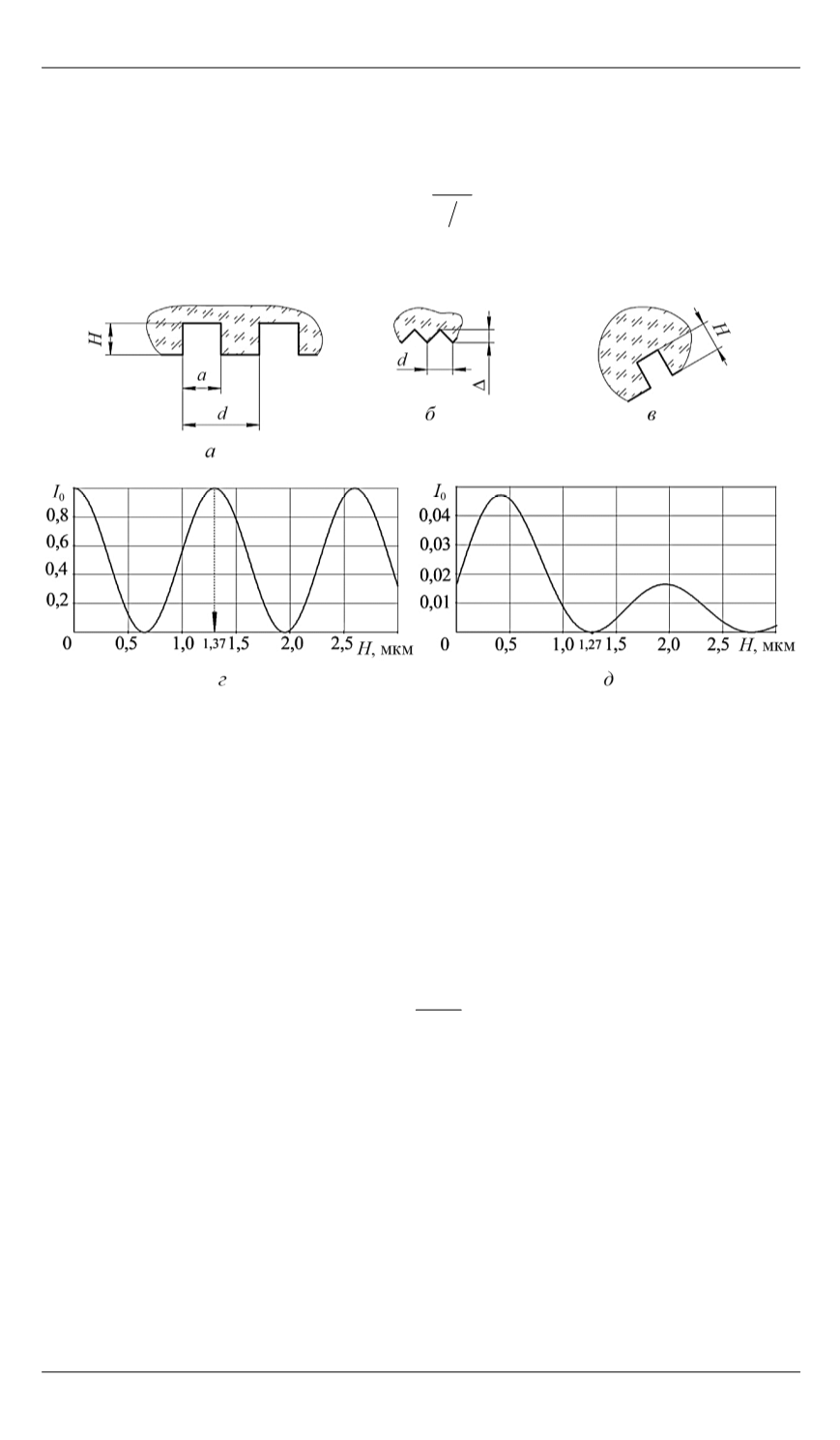
Рис. 5.
Фазовые дифракционные решетки с прямоугольным (
а
), треуголь-
ным (
б
) и эквивалентным (
в
) профилем, а также соответствующие (
г
,
д
)
относительные интенсивности нулевого порядка
На рис. 5,
б
представлена зависимость
I
0
(
H
) для
n
= 1,5,
λ
=
= 0,65 мкм и
ε
= 0, из которой следует, что максимум относительной
спектральной эффективности в нулевом порядке дифракции достига-
ется при
H
= 1,3 мкм. Таким образом, требуемая глубина
H
канавок
прямоугольного профиля, формируемая методом ПХТ (см. рис. 4,
б
),
.
1
H
n
λ=
−
(4)
Согласно второму условию для концентрации энергии эшелеттом
в направлении луча
1
(см. рис. 4,
г
) должен быть расположен мини-
мум интенсивности излучения, дифрагированного отдельным эле-
ментом.
Моделью для представленной на рис. 4,
г
эквивалентной схемы
является эшелетт фазовой дифракционной решетки с треугольным
профилем (см. рис. 5,
б
). Сопоставляя рис. 5 и рис. 4,
г
, можно счи-
тать, что глубина
Δ
треугольного рельефа такой фазовой решетки
sin
cos .
d
H
Δ = α + α
(5)


