Расчет нижней границы предельной нагрузки…
9
T
(1)
(1)
11
22 11 22 12
,
,
,
,
.
X X X X X X
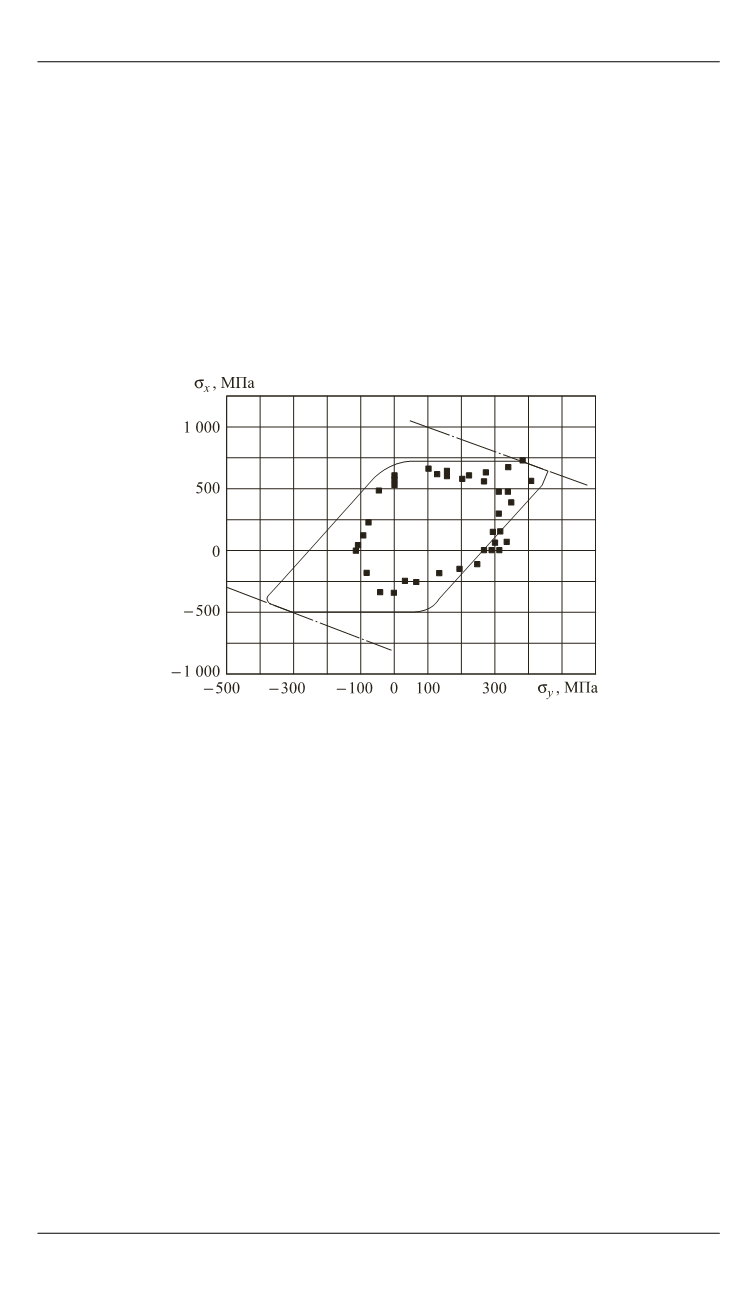
Результаты расчета для стеклопластика марки E-Glass/LY556/
HT907/DY063 со схемой армирования [90
/
30
], для которого
1
= 0,172;
= 0,828, приведены на рис. 6. Экспериментальные дан-
ные (точки) заимствованы из работы [10]. Характеристики прочности
монослоя таковы:
F
+1
= 1 150 MПa;
F
–1
= 750 MПa;
F
+2
= 40 MПa;
F
–2
= 150 MПa;
F
12
= 80 MПa. Предельная кривая получена расчетным
путем, прямые
1
2
x
y
F F
и
1
2
x
y
F F
показаны
штрихпунктиром.
Рис. 6.
Предельная кривая для стеклопластика со схемой армирования
[90
/
30
]
Следует отметить одно из достоинств предлагаемого подхода к
определению нижней границы предельной нагрузки. В ряде случаев,
согласно методу неравенств, из соотношений (1) и (2) следуют ана-
литические решения, которые могут быть востребованы при выпол-
нении проектных расчетов. Однако при большом числе переменных
решение задачи по методу неравенств приводит к чрезвычайно гро-
моздким преобразованиям и его применение становится нерацио-
нальным. Существенные упрощения получают при использовании
дополнительных гипотез относительно физико-механических свойств
волокнистых КМ. В частности, относительно простое решение мож-
но получить при введении в расчет нитяной модели монослоя, в со-
ответствии с которой параметрами
( )
( )
( )
2
2 12
,
,
i
i
i
F F F
можно пренебречь
по сравнению с
( )
1
i
F
,
( )
1
i
F
и принять, что
( )
( )
22
12
0.
i
i
В качестве примера воспользуемся нитяной моделью монослоя
для рассмотренного выше КМ со схемой армирования [0/90
/
].
Тогда из соотношений (1) имеем


