Расчет нижней границы предельной нагрузки…
7
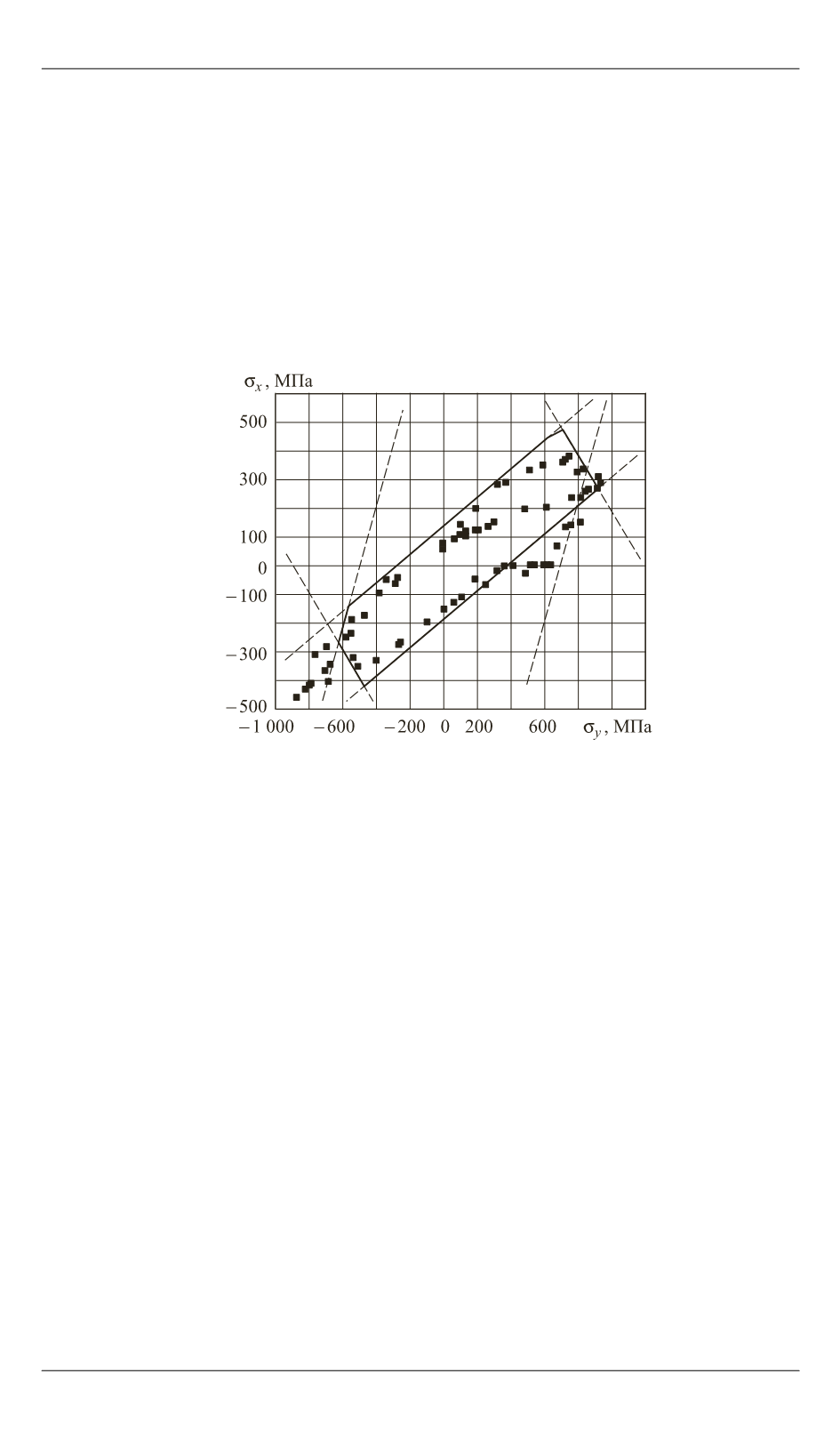
На рис. 4 область, соответствующая неравенствам (8), ограничена
штриховыми линиями, а ее границей является искомая предельная
кривая. Определенная в результате численного решения задачи
линейного программирования предельная кривая практически совпа-
ла с кривой, полученной из неравенств (8). В расчетах использованы
следующие прочностные характеристики монослоя:
F
+1
= 1 150 MПa;
F
–1
= 750 MПa;
F
+2
= 40 MПa;
F
–2
= 150 MПa;
F
12
= 80 MПa. Как видно
на рис. 4, теоретические результаты (сплошные линии) в целом удо-
влетворительно соответствуют экспериментальным данным (точки).
Рис. 4.
Предельная кривая для многослойного стеклопластика с углами
армирования
=
55
на плоскости напряжений
x
О
y
Рассмотрим многослойный КМ со схемой армирования [0/90
/
].
Здесь схема армирования такова:
n
= 4;
1
= 0,
2
=
/2,
3
= –
4
=
; относительные толщины монослоев
1
,
2
,
3
,
4
известны,
причем
3
=
4
=
/2, где
— толщина двойного спирального слоя.
Из третьего равенства (1) получаем соотношения
(1)
(2)
12
12
(3)
(4)
11
11
11
(3)
(4)
22
22
22
(3)
(4)
12
12
12
0;
;
;
.
Вектор переменных принимает вид
T
(1)
(1)
(2)
(2)
11
22 11
22
11 22 12
,
,
,
,
,
,
.
X X X X X X X X
Тогда ограничения (6) можно записать так:


