Б.С. Сарбаев
8
(1)
(2)
2
2
11 1
22 2
11
22
12
11
(1)
(2)
2
2
22 1
11 2
11
22
12
22
11
1
1
22
2
2
12
12
( )
( )
11
1
1
22
2
2
( cos
sin
sin 2 )
cos 0;
( sin
cos
sin 2 )
sin 0;
0
, 0
, 0
2 ,
0;
0
, 0
,
1
k
k
X X
X
X
X
C S
X X
X
X
X
C S
X F F X F F X F S
X F F X F F k
, 2,
где
2
2
11
1 1
2 2
1
2
12
2
2
22
2 1
1 2
1
2
12
( cos
sin
sin 2 ) ;
( sin
cos
sin 2 ) .
C F F F
F
F
C F F F
F
F
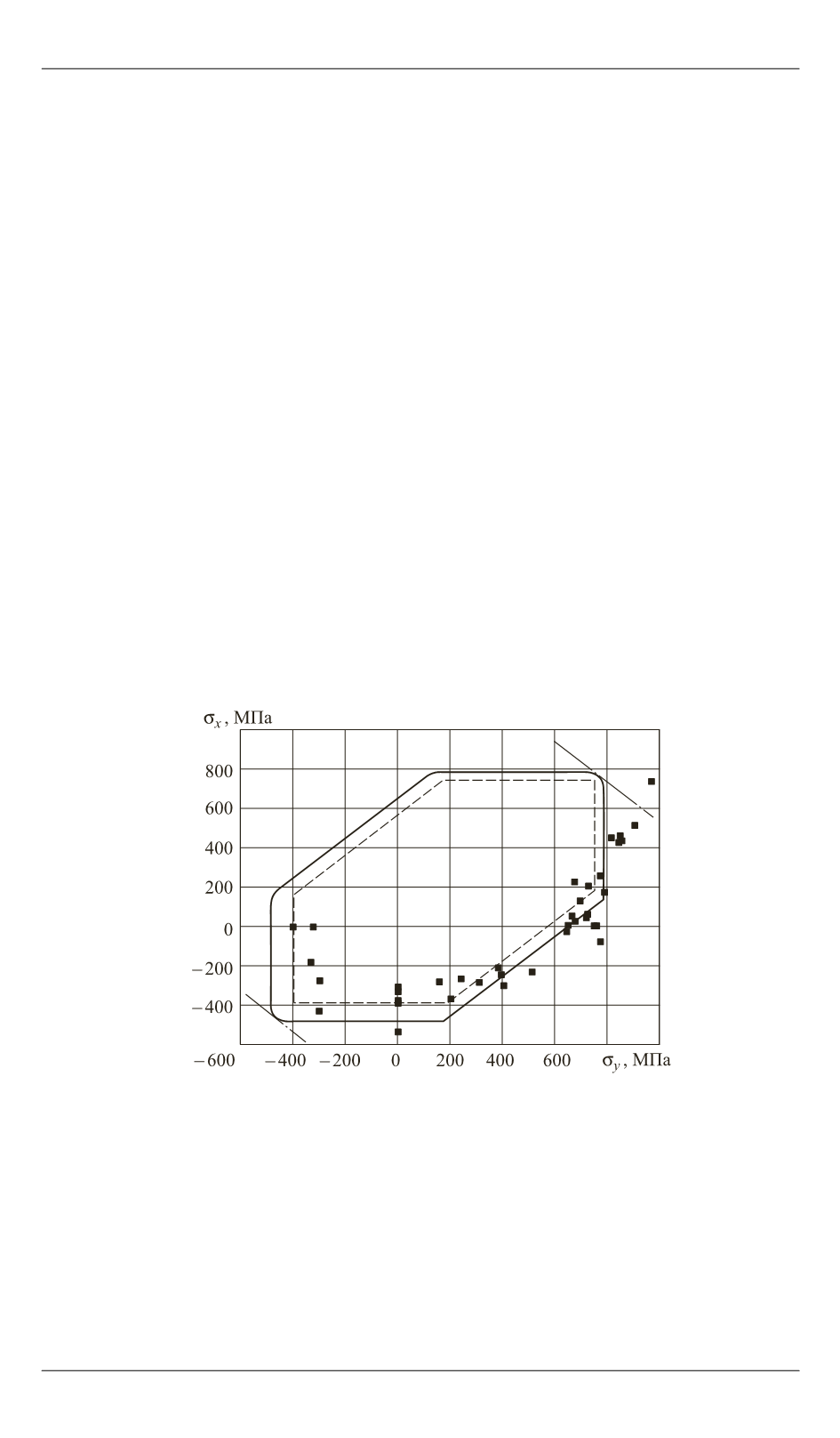
На рис. 5 изображена предельная кривая, полученная в результате
численного решения задачи для квазиизотропного углепластика марки
AS4/5301-6 со схемой армирования [90
/
45
/0], т. е. при
=
/4;
1
=
=
2
=
3
=
4
= 0,25. При расчете были приняты такие прочностные ха-
рактеристики монослоя:
F
+1
= 1 500 MПa;
F
–1
= 800 MПa;
F
+2
= 40 MПa;
F
–2
= 135 MПa;
F
12
= 40 MПa. По-прежнему точками обозначены экспе-
риментальные данные из работы [10]. Как и следовало ожидать, пре-
дельная кривая в соответствии с неравенством (3) расположена между
двумя параллельными прямыми
1
2
x
y
F F
и
1
x
F
2
,
y
F
которые на рис. 5 показаны штрихпунктирными линиями.
Рис. 5.
Предельная кривая для квазиизотропного углепластика со схемой
армирования [90
/
45
/0] на плоскости напряжений
x
О
y
Проведем анализ прочностных характеристик многослойного КМ
со схемой армирования [90
/
]. В этом случае имеем
n
= 3;
1
=
/2,
2
= –
3
=
относительные толщины монослоев
1
,
2
,
3
известны,
причем
2
=
3
=
/2. Аналогично предыдущему случаю здесь также
можно получить частный случай ограничений (6). При этом вектор
переменных будет иметь следующий вид:


