А.С. Романов, А.В. Семиколенов
2
жидкости пропорциональна градиенту химического потенциала мо-
лекул жидкости вблизи линии трехфазного контакта.
Настоящая работа посвящена проблеме определения динамиче-
ского угла смачивания, существование которого подтверждают экс-
перименты [4]. Для этого проводится асимптотическое исследование
формы свободной поверхности жидкости вблизи линии трехфазного
контакта. В результате дается определение динамического (т. е. зави-
сящего от скорости растекания) угла смачивания и найден асимпто-
тический закон, связывающий этот динамический угол смачивания и
скорость растекания. Применение развиваемой теории продемон-
стрировано на примере расчета скорости безнапорного заполнения
плоского капилляра частично смачивающей жидкостью.
В приближении теории смазки форма свободной поверхности од-
номерной жидкой пленки, растекающейся вдоль гладкой твердой по-
верхности при частичном смачивании, описывается уравнением
( )
2
3
2
1
0
3
h
h
h
h
t
x
x x
x
α
⎡
⎤
∂Φ
⎛
⎞
∂
∂
∂ ∂
+
σ −
=
⎢
⎥
⎜
⎟
∂ μ ∂
∂ ∂
∂
⎢
⎥
⎝
⎠
⎣
⎦
,
(1)
где
( , )
h x t
— толщина слоя жидкости над твердой поверхностью;
x
,
t
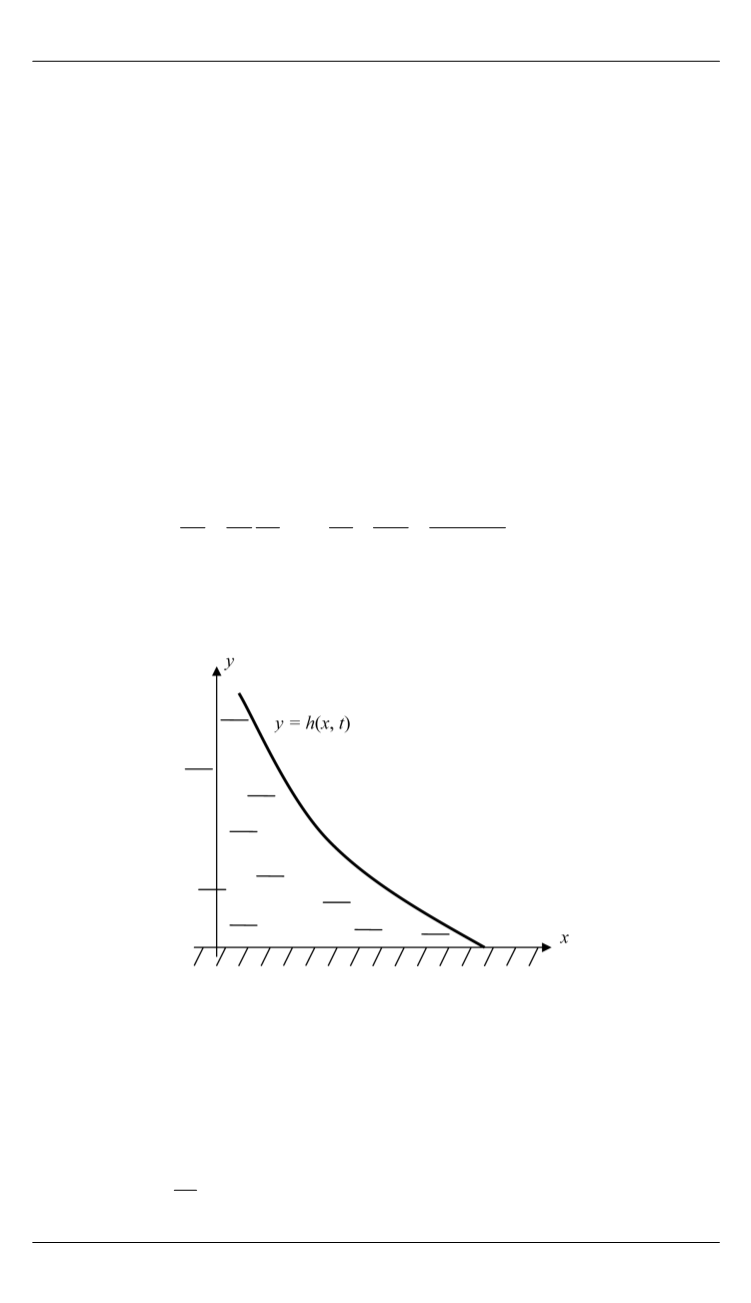
— координата, вдоль которой растекается жидкость (рис. 1) и вре-
мя соответственно;
μ
— динамическая вязкость;
σ
— поверхностное
натяжение; функция
( )
h
α
Φ
определяет зависимость расклинивающе-
го давления (или, с точностью до знака, химического потенциала мо-
лекул жидкости, рассчитанного на единицу объема):
( )
(
)
( )
(
)
3 2
.
12
LL L S LS
L S LS
L
h
h n a n n a G n n a G
−
α
π
⎡
⎤
Φ =
−
α −
π − α
⎣
⎦
(2)
Рис. 1.
Форма свободной поверхности жидкости


