
А.А. Валишин
12
Инженерный журнал: наука и инновации
# 11·2017
берегов. На верхнем берегу трещины и в непосредственной близости от
него возникает зона повышенной температуры. Из формулы (7) в без-
размерных координатах для области вблизи верхнего берега получаем
2
2
2
0
2
2
( , )
1 1
.
4 (1 )
+ µ
µ ε = +
−µ +
ε
λ
−µ
T
T
q
T
T l
(17)
Наибольшее повышение температуры достигается в середине
верхнего берега
( 0):
µ =
2
0
1
(0, )
1
.
2
ε = +
+ ε
λ
T
T
q
T
T l
(18)
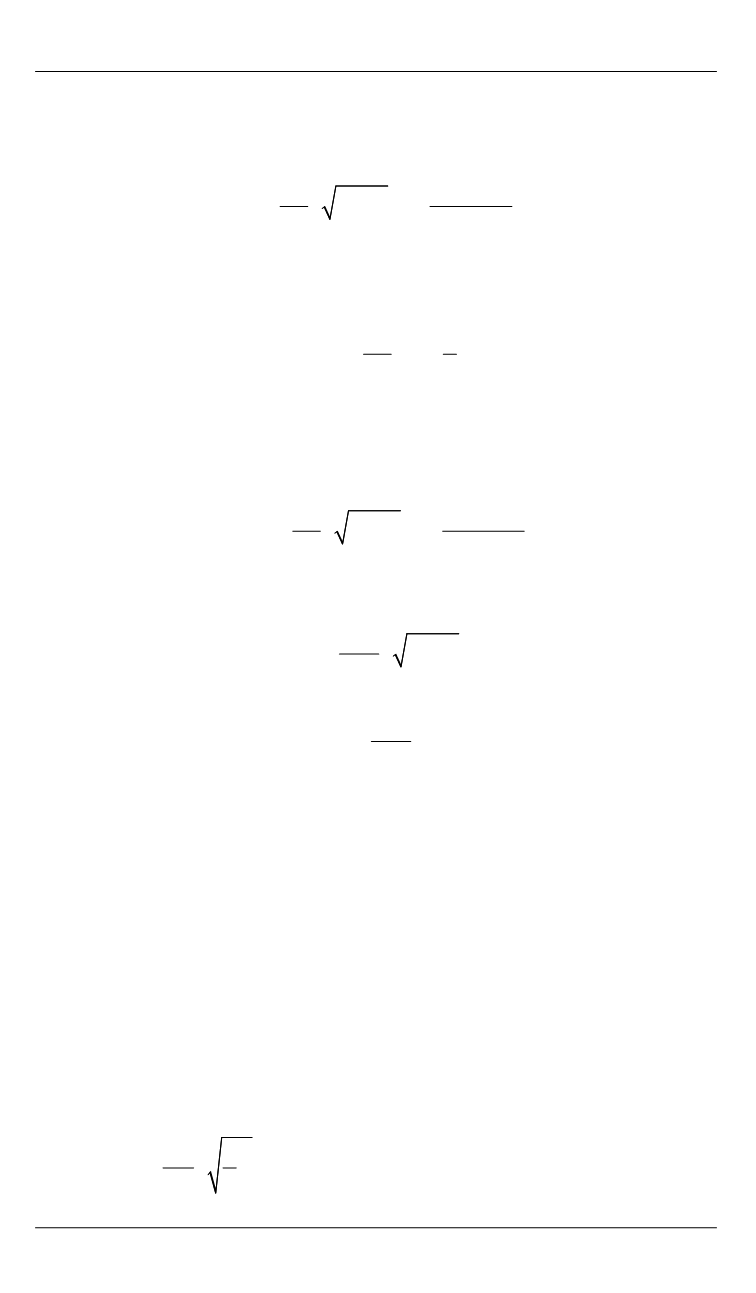
Под трещиной находится зона пониженной температуры, не
превышающей начальную
Т
0
. Это зона частичной «тепловой тени»,
где температура
(
)
2
2
2
0
2
2
( , )
1 1
.
4 1
+ µ
µ ε = −
−µ +
ε
λ
−µ
T
T
q
T
T l
(19)
Скачок температуры на берегах трещины
2
2 ( )
1 ,
∆ µ =
−µ
λ
T
T
q
T
l
(20)
его наибольшее значение
max
2 .
∆ =
λ
T
T
q
T
l
(21)
По мере приближения к вершинам трещины скачок температуры
стремится к нулю. Величина температурного скачка на берегах
трещины определяется мощностью воздействующего теплового
потока
T
q
и длиной трещины
.
l
Численная оценка для ПММА дает
значение
max
∆
T
от десятых долей градуса до нескольких градусов, но
по мере приближения к вершинам трещины температуры ее берегов
выравниваются.
Рассмотрим детальнее распределение температуры и теплового
потока вблизи вершин трещины. Для этого перейдем в полярную
систему координат, поместив ее начало в правую вершину трещины
(см. рис. 2). В окрестности левой вершины ситуация будет
аналогичной. Распределение температуры в полярных координатах
имеет вид
[
]
1/2
0
1
( , )
( , cos ) 2(1 cos ) cos
sign ,
2
ξ θ = +
ξ Φ ξ θ − + ξ θ θ + ξ
θ
λ
T
T
q
T
T l
(22)
















