
Возмущение температурного поля трещиной в полимерных материалах
Инженерный журнал: наука и инновации
# 11·2017 9
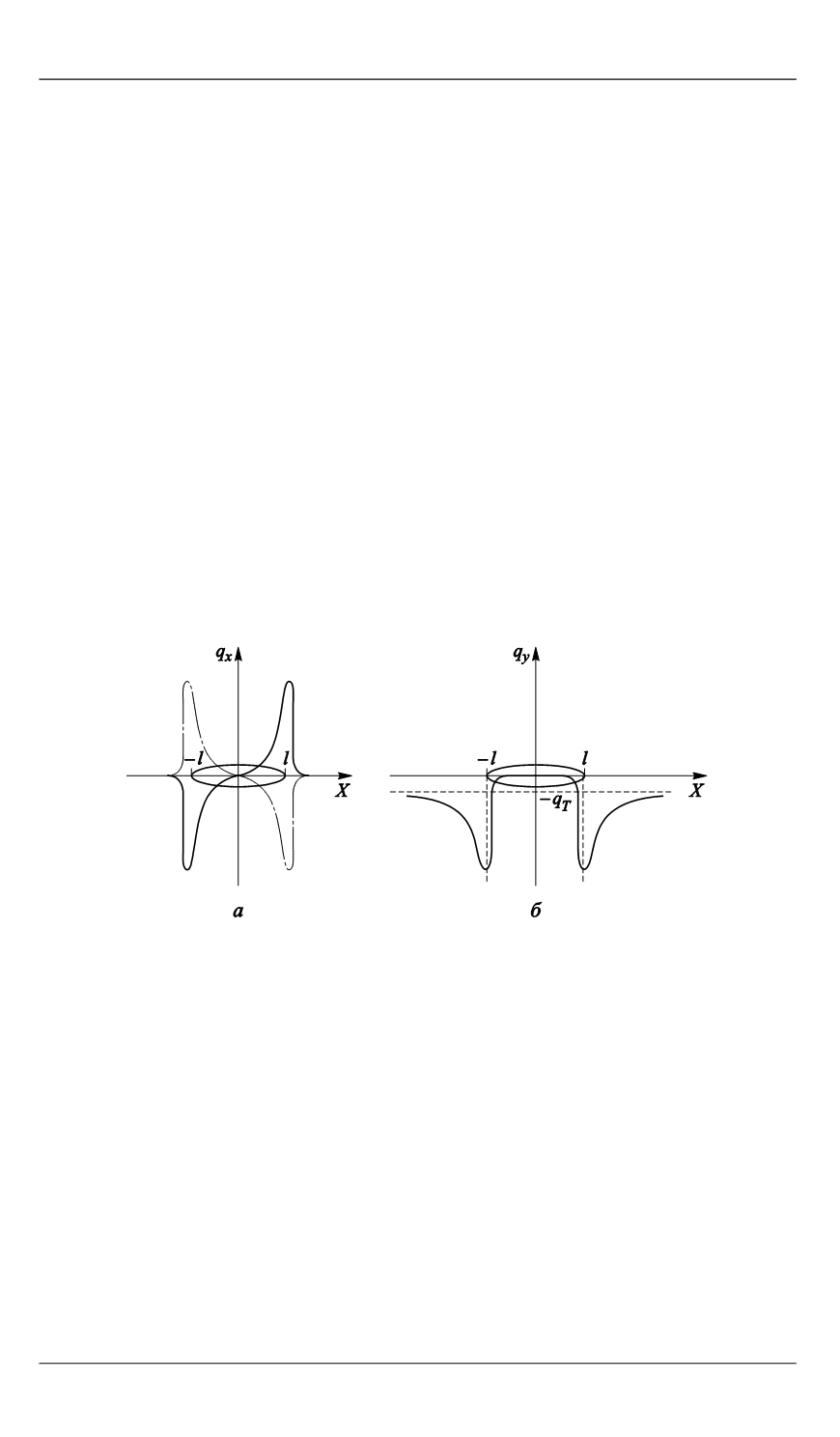
На рис. 6 показана схема зависимости компонент
x
q
и
y
q
вектора
плотности теплового потока от координаты
x
на верхнем и нижнем
берегах трещины. На верхнем берегу тангенциальная компонента
x
q
неограниченно возрастает по абсолютной величине с приближением
к вершинам трещины. Вне трещины тангенциальная компонента
x
q
всюду равна нулю. Нормальная компонента
y
q
, наоборот, внутри
трещины отсутствует, а вне трещины по мере удаления от вершин
быстро убывает по абсолютной величине от бесконечного значения
до уровня, соответствующего отсутствию трещины.
Появление бесконечностей для компонент вектора плотности
теплового потока
q
— это следствие несовершенства принятой
модели трещины. В действительности трещина, конечно же, не
является математическим разрезом, не имеющим толщины. В
наиболее совершенной модели хрупкой трещины трещина
рассматривается как щель с асимптотически сходящимися берегами.
Поэтому физически реальная картина распределения теплового
потока соответствует рис. 7.
Рис. 7.
Распределение тангенциальной (
а
) и нормальной (
б
)
компонент вектора плотности теплового потока по ширине
образца в окрестности реальной трещины:
сплошная линия
— верхний берег;
штрихпунктирная линия
— нижний берег
Тангенциальная компонента
x
q
с приближением к вершинам
трещины изнутри самой трещины довольно медленно возрастает по
абсолютной величине до большого, но конечного значения, а вне
трещины очень быстро спадает до нуля (рис. 7,
а
). Для нормальной
компоненты
y
q
картина будет соответствовать рис. 7,
б
, т. е. вне
трещины нормальная компонента медленно уменьшается по абсо-
лютной величине до значения
T
q
, отвечающего состоянию без
трещины, а внутри трещины с приближением к ее вершинам резко
















