
А.А. Валишин
18
Инженерный журнал: наука и инновации
# 11·2017
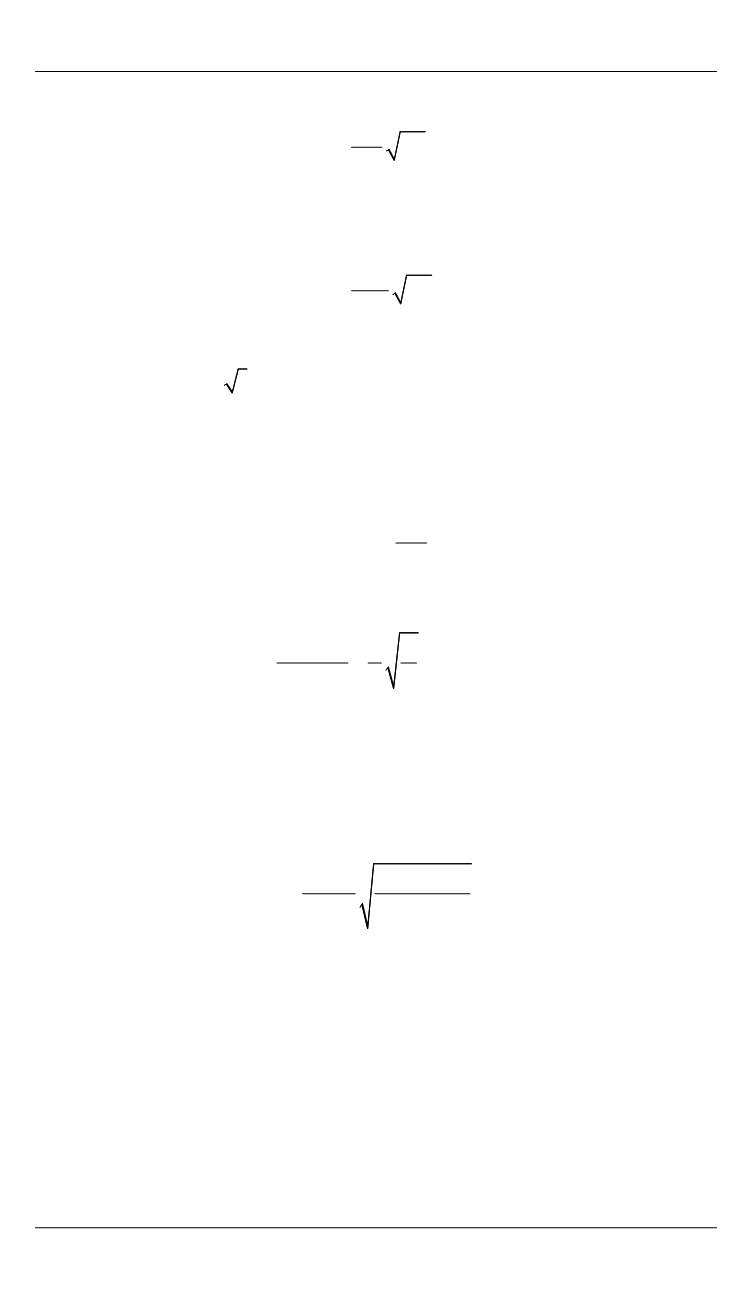
Отсюда перегрев «клюва» в области верхнего берега
.
∆ =
λ
T
T
q T
l d
(36)
В области «клюва» температура верхнего и нижнего берегов
одинакова, значит, выражение нужно удвоить. Окончательно пе-
регрев «клюва»
2
.
∆ =
λ
T
T
q T
l d
(37)
Видно, что перегрев «клюва» зависит от размера трещины,
увеличиваясь как
l
. На флуктуационной стадии развития размер
трещины увеличивается в 6–10 раз, поэтому по мере роста трещины
перегрев «клюва» увеличивается в 2,4–3,2 раза.
Сравним температуру «клюва» с максимальной температурой
верхнего берега в его середине. Из формулы (18) получаем
берег 0
.
= +
λ
T
T
q
T T l
(38)
Сопоставляя (38) с (37), получаем
берег
1 1, 44,
2
Т
l
Т
d
∆
= ≈
∆
(39)
т. е. максимальная температура на верхнем берегу почти в 1,5 раза
превышает температуру «клюва». Этого достаточно, чтобы обеспечить
постоянный приток теплоты в «клюв» по мере роста трещины.
В заключение выразим перегрев «клюва» через параметры,
определяющие его размер в формуле (33). Получаем
2
2
.
(1 )
λ π
∆ =
λ
− ν α
T
T
п
q
l E
T
(40)
Таким образом, если при механическом нагружении в «клюв»
трещины идет постоянный поток упругой энергии, то при тепловом
нагружении — поток тепловой энергии. Оба потока способствуют
термофлуктуационным элементарным актам разрушения, и развитие
трещины постепенно ускоряется вплоть до полного разрушения.
Выводы.
1. При действии установившегося теплового потока в образце с
трещиной значительно увеличиваются температурные напряжения,
что вызвано локальным возрастанием температурного градиента в
окрестности трещины.
















