
В.М. Балык, А.А. Маленков, В.С. Петровский, А.С. Станченко
4
Инженерный журнал: наука и инновации
# 10·2017
Статистическая выборка (табл. 1), по которой осуществляется
синтез устойчивого проектного решения, формируется с помощью
зондирования математических моделей (1) и (2)
N
испытаниями.
Каждое испытание характеризуется двумя векторами проектного ре-
шения
i
a
и
1
i
a
+
,
1,
1
i
N
= −
.
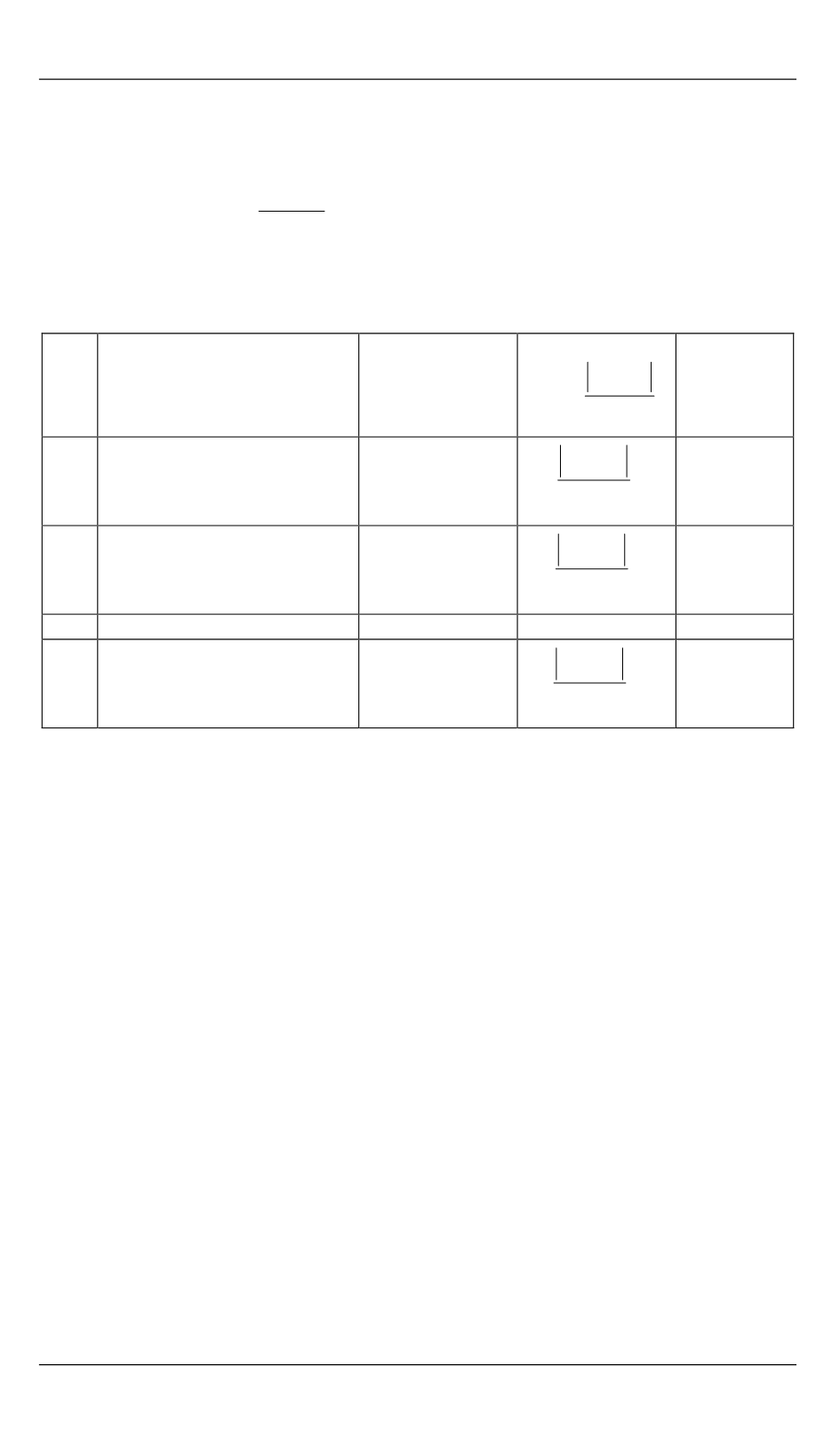
Таблица 1
Синтез устойчивого проектного решения
№
п/п
Вектор проектного решения
a
Критерий опти-
мальности
J
Константа Лип-
шица
i
j
i
j
J J
a a
−
−
Заданная
константа
Липшица
зад
K
1
(
)
1
0 кр корп 1
,
,
,
a n l l
m
=
(
)
2
0 кр корп 2
,
,
,
a n l l
m
=
1 нак1
J P
=
2 нак2
J P
=
1
i
j
i
j
J J
a a
−
−
1, зад
K
2
(
)
3
0 кр корп 3
,
,
,
a n l l
m
=
(
)
4
0 кр корп
4
,
,
,
a n l l
m
=
3 нак3
J P
=
4 нак4
J P
=
2
i
j
i
j
J J
a a
−
−
2, зад
K
…
…
…
…
…
N
(
)
1
0 кр корп
1
,
,
,
N
N
a
n l l
m
−
−
=
(
)
0 кр корп
,
,
,
N
N
a n l l
m
=
1 нак 1
N
N
J
P
−
−
=
нак
N
N
J P
=
i
j
i
j
N
J J
a a
−
−
, зад
N
K
Статистическая выборка (см. табл. 1) имеет ряд особенностей.
В каждой строке выборки задаются два варианта проектного реше-
ния, которые необходимы для расчета условия устойчивости. Для
всех строк выборки значения заданной константы Липшица
зад
K
принимаются одинаковыми, т. е.
1, зад
2, зад
, зад
.
N
K K
K
=
=…=
Это необходимое условие вероятности выполнения целевой зада-
чи всей динамической системой в целом не ниже заданной. Таким
образом, осуществляется постановка задачи выбора проектного ре-
шения, при котором суммарная эффективность системы крылатых
ракет не ниже заданной —
P
Σ
при любой вариации неконтролируе-
мых факторов
ω
из заданного множества
.
W
Расчет вероятности накрытия цели.
Траекторию полета каж-
дой ракеты можно описать по следующим участкам: набора высоты,
маршевому участку, участку наведения, низковысотному участку.
В процессе движения два раза происходит включение радиолокаци-
онной головки самонаведения (ГСН). При первом включении ГСН
происходит захват и селекция целей. Посредством обмена информа-
















