
Оптимизация экспедиции к Фобосу космических аппаратов с комбинированной тягой…
Инженерный журнал: наука и инновации
# 7·2017 13
ная задача многоэкстремальна, для поиска области, в которой следует
искать локально оптимальное решение, необходимо предварительно
провести глобальную оптимизацию. Для этого сначала задача иссле-
довалась на основе решения серии задач Ламберта с учетом одного
притягивающего центра на каждом участке перелета [23, 24], а затем
решалась в импульсной постановке на основе принципа Лагранжа.
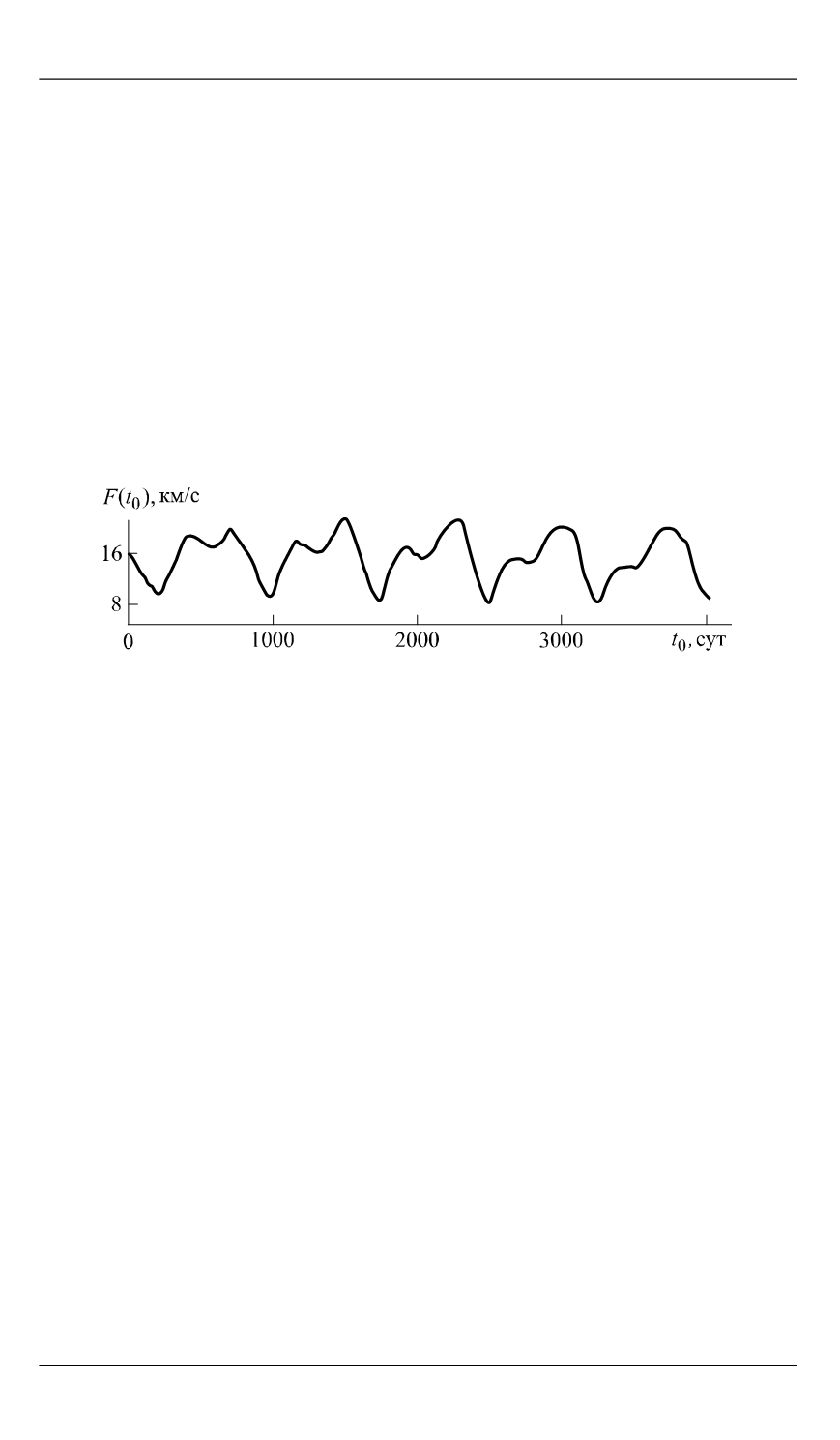
В результате проведенного анализа для импульсного случая (рис. 2)
получена окрестность экстремалей с лучшим значением функциона-
ла, в которой далее уже можно решать задачу с ограниченной тягой
[25]. К тому же из рисунка видно, что окна старта к Марсу есть каж-
дые два года, время старта
t
0
отсчитывается от 1 января 2020 г.,
а лучший функционал оказался у экспедиции со стартом в 2026 г.
Рис. 2.
Окна старта к Марсу в период 2020–2030 гг.:
F
(
t
0
) —
сумма модулей импульса у Земли и двух импульсов у Марса в импульсной
задаче оптимизации экспедиции;
t
0
—
время старта
При исследовании задачи в упрощенной постановке выявлено,
что КА на Фобосе выгодно «сидеть» около одного земного года.
А значит,
TF
в условии (16) обращается в нуль, и исходную задачу
можно в окрестности данного предполагаемого локального миниму-
ма легко разбить на две независимые: задачу «вперед» и задачу
«назад», причем совокупность их решений будет экстремалью в об-
щей задаче.
После получения начального приближения траектории строились
следующим образом. Задачу перелета «вперед» просчитывали с двух
концов
0
(
t
и
1
)
t
в середину траектории
t
(рис. 3), затем задачу пере-
лета «назад» считали от
2
t
к
3
t
. В качестве параметров пристрелки
выбирались 12–14 значений:
0
r
,
0
Ω
,
0
,
1 0
( ),
t
1 0
( ),
t
3 1
( ),
t
3 1
( ),
t
3 1
( ),
x
p t
3 1
( ),
y
p t
3 1
( ),
z
p t
k
,
где
k
— моменты включения и отклю-
чения малой тяги в задаче «вперед», при исследовании задачи на тра-
екториях реализовывалось управление с двумя или тремя активными
участками малой тяги, тогда
2
k
или
k
=
4
соответственно. И семь
параметров пристрелки:
ДУВА
Δ ,
3
t
и
4
,
x
p
4
,
y
p
4
,
z
p
4
,
4
при
















