
Фильтрация жидкости в неоднородном слое с коэффициентом фильтрации…
Инженерный журнал: наука и инновации
# 6·2017 9
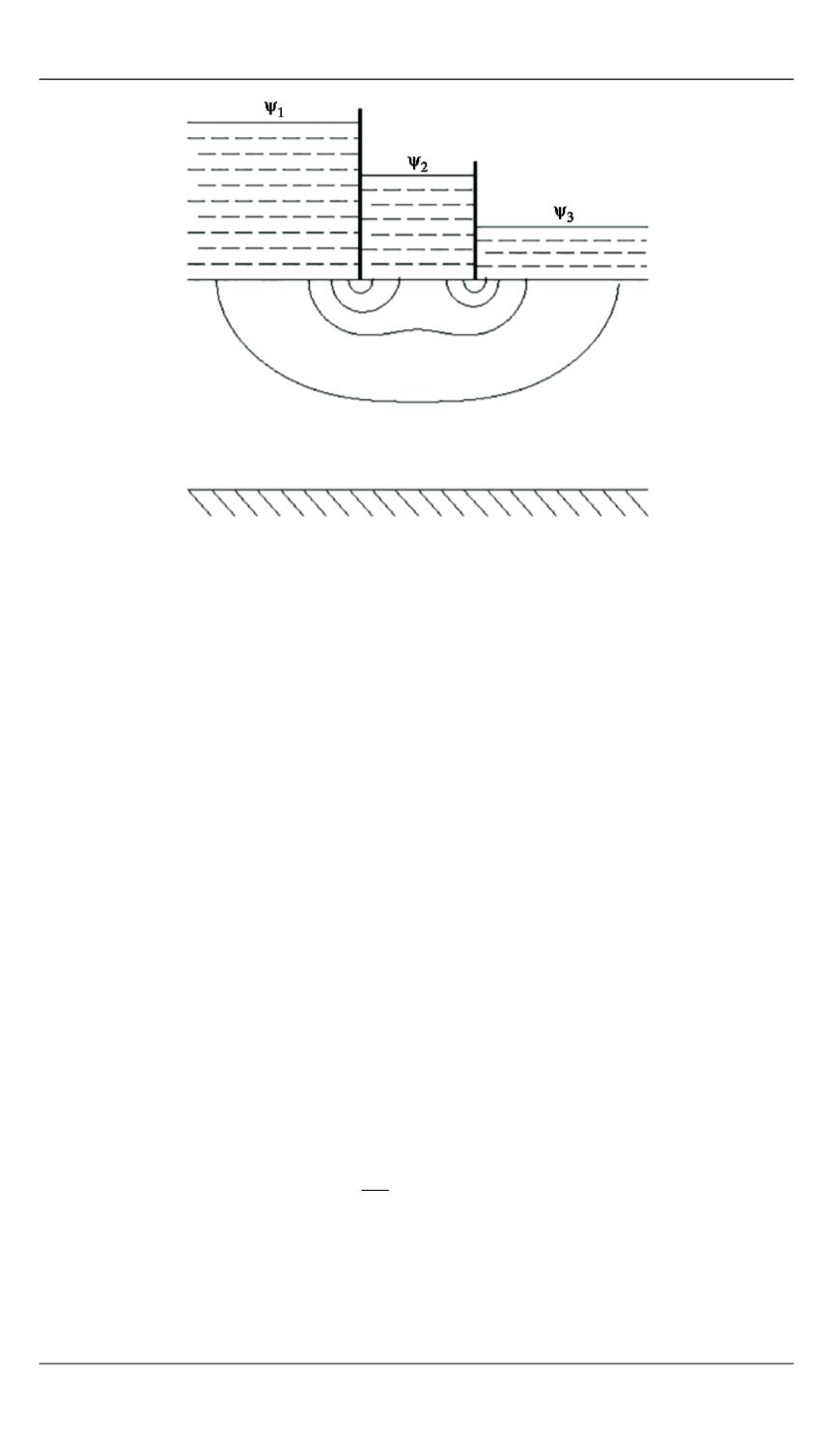
Рис. 5.
Линии тока фильтрационного течения под
каскадом из двух точечных плотин в неоднородном
слое
0
,
y
< < π
1,
b
=
1
3,
ψ = −
2
2,
ψ = −
3
1
ψ = −
с коэффициентом фильтрации
K
=
у
2
Источник (сток) в трехмерном неоднородном слое.
Рассмот-
рим задачу, в которой между двумя плоскостями находится источник
(сток) интенсивности
Q
. Нижняя плоскость изолирована, а верхняя
есть плоскость равного потенциала [1, 5]. В нашем неоднородном
случае имеем задачу
2
0
0
div( grad ( , ))
(
) (
),
y
u x y Q x x y y
= a − a −
(17)
2
1 2
0
( , )
, 0
, 0
,
x x x
y a y a
=
∈ < < < <
2
2
0
lim
,
0, ( , ) 0,
(
.
)
y
y
y u x y
u x a
x
→(
=
= ∈
(18)
Переходя к функции
( , ) ( , ),
v x y y u x y
=
получаем для нее задачу
Дирихле для уравнения Пуассона:
0
0
0
Δ ( , )
(
) (
),
Q v x y
x x y y
y
= δ − δ −
2
0
, 0
, 0
,
x
y a y a
∈ < < < <
2
( , 0) 0, ( , ) 0,
.
v x
v x a x
=
= ∈
















