
Фильтрация жидкости в неоднородном слое с коэффициентом фильтрации…
Инженерный журнал: наука и инновации
# 6·2017 13
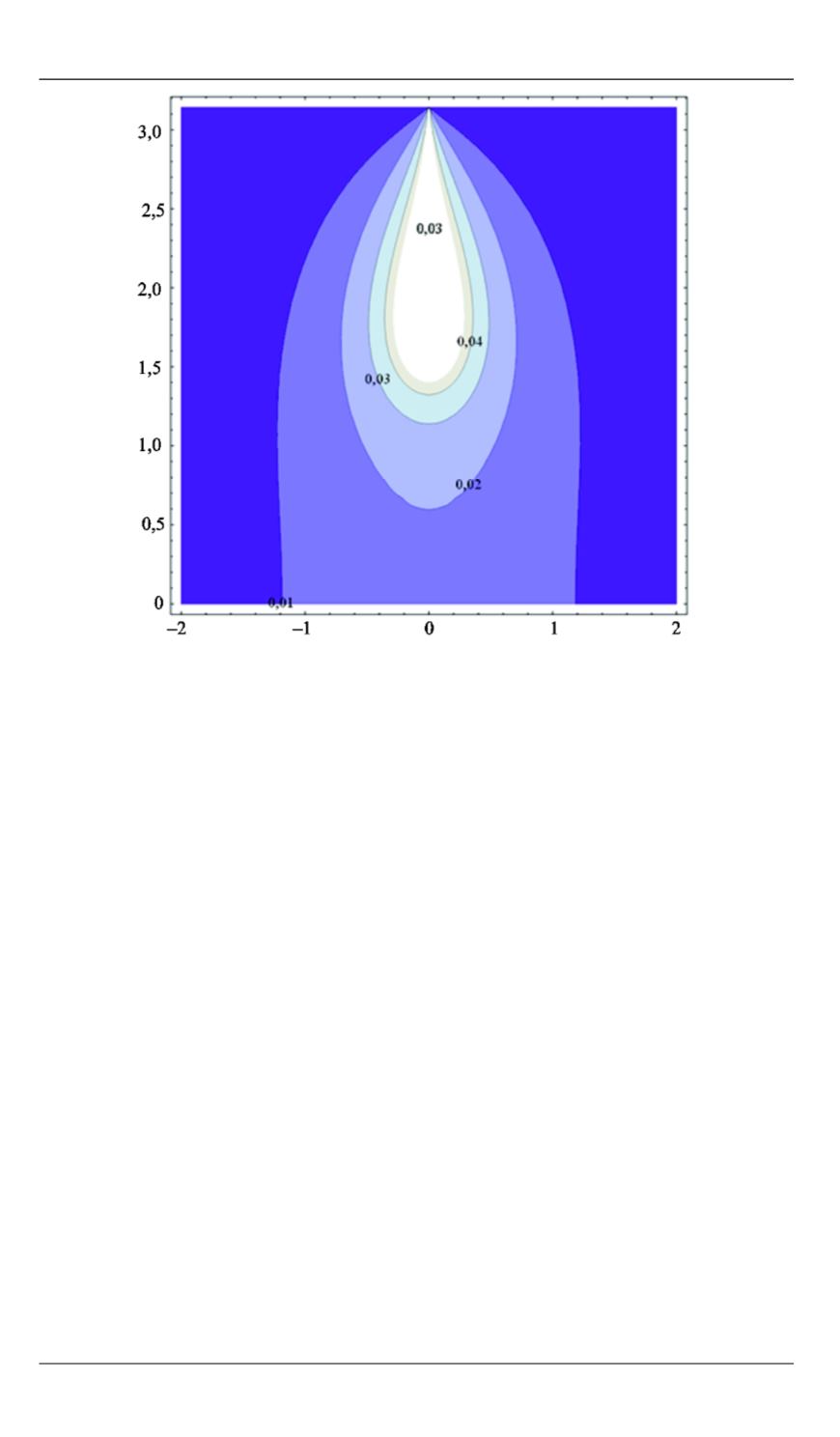
Рис. 8.
Сечения поверхностей равного потенциала вертикаль-
ной скважины в неоднородном слое с коэффициентом фильтра-
ции
K
=
y
2
плоскостями, проходящими через ось
y
Заключение.
Рассмотрена модельная задача фильтрации в неод-
нородном слое (в плоскопараллельном и пространственном случаях)
с коэффициентом фильтрации
2
( , )
K x y y
=
, где
y
— вертикальная
координата. Задача решена аналитически. Это позволило смоделиро-
вать стационарные процессы фильтрации жидкости под точечной
плотиной и каскадом из двух плотин в полосе с водоупором, а в про-
странственном случае — фильтрацию жидкости к вертикальной
скважине. Потенциал скорости при этом записывается в виде инте-
грала от элементарных функций, а в рассмотренных примерах плос-
ких задач эти интегралы вычисляются в элементарных функциях.
Предложенный метод позволил найти аналитическое решение рас-
сматриваемой задачи, а в некоторых примерах эти решения содержат
только элементарные функции.
Предложенный метод решения краевых задач можно применить
и при рассмотрении стационарных электрических и тепловых полей
в неоднородных средах, в которых, соответственно, диэлектрическая
проницаемость и коэффициент теплопроводности изменяются по
квадратичному закону.
















